
如图,AB=CD,点E、F分别是BC、AD中点,延长BA,CD分别与EF的延长线交于点P、Q,则BP与CQ的大小关系是BP CQ(填“>”“<”“=”)
。
=
【解析】
试题分析:连接BD,取BD的中点M,连接EM、FM,延长QE到点O,使QE=OE,则可证得△BOE≌△COQ,所以BO=CQ,∠O=∠CQF,根据三角形的中位线性质可得FM//AB且FM=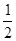 AB,EM//CD且EM=
AB,EM//CD且EM=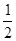 CD,再结合AB=CD可得EM=FM,即可证得∠MEF=∠MFE,再根据平行线的性质可得∠BPF=∠CQF,问题得证.
CD,再结合AB=CD可得EM=FM,即可证得∠MEF=∠MFE,再根据平行线的性质可得∠BPF=∠CQF,问题得证.
连接BD,取BD的中点M,连接EM、FM,延长QE到点O,使QE=OE,
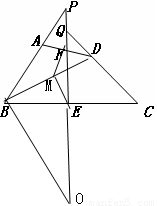
则可证得△BOE≌△COQ
所以BO=CQ,∠O=∠CQF
因为F是AD的中点
所以FM是△ABD的中位线
所以FM//AB且FM=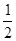 AB
AB
同理EM//CD且EM=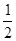 CD
CD
因为AB=CD
所以EM=FM
所以∠MEF=∠MFE
因为∠BPF=∠MFE,∠CQF=∠MEF
所以∠BPF=∠CQF
因为∠O=∠CQF
所以∠BPF=∠O
所以BP=BO
因为BO=CQ
所以BP=CQ.
考点:三角形的中位线定理,平行线的性质
点评:解题的关键是熟记三角形的中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源:学习周报 数学 沪科八年级版 2009-2010学年 第19~26期 总175~182期 沪科版 题型:013
如图,AB=CD,AD与CB交于点O,要使△AOB≌△COD,则需要添加的一个条件可以是

A.AO=CO
B.BO=DO
C.CB=AD
D.∠A=∠C
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江建德李家镇初级中学八年级5月单元检测数学试卷(带解析) 题型:填空题
如图,AB=CD,点E、F分别是BC、AD中点,延长BA,CD分别与EF的延长线交于点P、Q,则BP与CQ的大小关系是BP CQ(填“>”“<”“=”) 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com