
【题目】如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.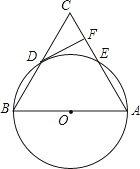
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求 ![]() 的长(结果保留π).
的长(结果保留π).
【答案】
(1)
证明:连接OD,如图所示.
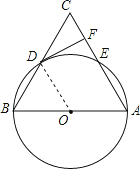
∵DF是⊙O的切线,D为切点,
∴OD⊥DF,
∴∠ODF=90°.
∵BD=CD,OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC,
∴∠CFD=∠ODF=90°,
∴DF⊥AC
(2)
解:∵∠CDF=30°,
由(1)得∠ODF=90°,
∴∠ODB=180°﹣∠CDF﹣∠ODF=60°.
∵OB=OD,
∴△OBD是等边三角形,
∴∠BOD=60°,
∴ ![]() 的长=
的长= ![]() π
π
【解析】(1)连接OD,由切线的性质即可得出∠ODF=90°,再由BD=CD,OA=OB可得出OD是△ABC的中位线,根据三角形中位线的性质即可得出,根据平行线的性质即可得出∠CFD=∠ODF=90°,从而证出DF⊥AC;(2)由∠CDF=30°以及∠ODF=90°即可算出∠ODB=60°,再结合OB=OD可得出△OBD是等边三角形,根据弧长公式即可得出结论. 本题考查了切线的性质、弧长公式、平行线的性质、三角形中位线定理以及等边三角形的判断,解题的关键是:(1)求出∠CFD=∠ODF=90°;(2)找出△OBD是等边三角形.本题属于中档题,难度不大,解决该题型题目时,通过角的计算找出90°的角是关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
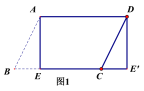
【题目】(1)如图1,纸片![]() ABCD中,AD=5,
ABCD中,AD=5,![]() ,过点A作AE⊥BC,垂足为E,沿AE剪下
,过点A作AE⊥BC,垂足为E,沿AE剪下![]() ,将它平移至
,将它平移至![]() 的位置,拼成四边形
的位置,拼成四边形![]() ,则四边形
,则四边形![]() 的形状为(_____)
的形状为(_____)
A.平行四边形 B.菱形 C.矩形 D.正方形
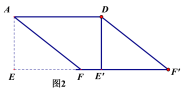
(2)如图2,在(1)中的四边形![]() 中,在EF上取一点P,EP=4,剪下
中,在EF上取一点P,EP=4,剪下![]() ,将它平移至
,将它平移至![]() 的位置,拼成四边形
的位置,拼成四边形![]() 。①求证:四边形
。①求证:四边形![]() 是菱形;②求四边形
是菱形;②求四边形![]() 的两条对角线的长。
的两条对角线的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两名运动员,选择一人参加市射击比赛,在选拔赛上,每人打10发,其中甲的射击成绩分别为10、8、7、9、8、10、10、9、10、9
①计算甲的射击成绩的方差;
②经过计算,乙射击的平均成绩是9,方差为1.4,你认为选谁去参加市射击比赛合适,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,一蔬菜经营户用114元从蔬菜批发市场购进黄瓜和土豆共40kg到菜市场去卖,黄瓜和土豆这天的批发价和零售价(单位:元/kg)如下表所示:
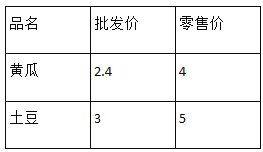
(1)他当天购进黄瓜和土豆各多少千克?
(2)如果黄瓜和土豆全部卖完,他能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为点D,点C的对应点为点E,连接BD,BE.
(1)如图,当α=60°时,延长BE交AD于点F.
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
③请直接写出BE的长;
(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从甲、乙、丙、丁四名学生中选一名参加“汉字听写”大赛,选拔中每名学生的平均成绩 ![]() 及其方差s2如表所示,如果要选拔一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
及其方差s2如表所示,如果要选拔一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
甲 | 乙 | 丙 | 丁 | |
| 8.9 | 9.5 | 9.5 | 8.9 |
s2 | 0.92 | 0.92 | 1.01 | 1.03 |
A.甲
B.乙
C.丙
D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
(1)求证:△OAE≌△OBG.
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(k+1)x+2k﹣2=0.
(1)求证:此方程总有两个实数根;
(2)若此方程有一个根大于0且小于1,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com