
��֪����A��B�ֱ���ֱ������ϵ��x��y����������ϣ�O������ԭ�㣬��C������AO�ϣ���D���߶�OB�ϣ�ֱ��AD���߶�BC�ཻ�ڵ�P����![]() ��a��
��a��![]() ��b��
��b��![]() ��k��
��k��
(1)��ͼ1����a��![]() ��b��1ʱ�������k��ֵ��
��b��1ʱ�������k��ֵ��

(2)��a��![]() ��b��1ʱ(��ͼ2)�������k��ֵ����a��
��b��1ʱ(��ͼ2)�������k��ֵ����a��![]() ��b��
��b��![]() ʱ��k��________��
ʱ��k��________��

(3)��������̽���о����������������⣺����ֱ��д���ú�a��b����ʽ��ʾk��________��������A(8��0)����B(0��6)��C(��2��0)��ֱ��ADΪ��y����![]() x��4����k��________��
x��4����k��________��
 �ŵ������ϵ�д�
�ŵ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| AC |
| AO |
| BD |
| DO |
| CP |
| PB |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 5 |
| 15 |
| 2 |
| 15 |
| 2 |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������̲�ȫ�⡡��ѧ�����꼶�ϲᡡ(���տư�) �տư� ���ͣ�047
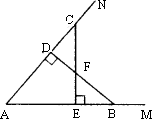
��ͼ����֪����B��C�ֱ��ڡ�MAN�������ϣ�BD��AN��CE��AM������ֱ�ΪD��E��BD��CE�ཻ�ڵ�F����BF��CF��
��֤����F�ڡ�MAN��ƽ�����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012���㽭�������������ѧ�п�ģ����ѧ�Ծ����������� ���ͣ������
��֪����A��B�ֱ���ֱ������ϵ��x��y����������ϣ�O������ԭ�㣬��C������AO�ϣ���D���߶�OB�ϣ�ֱ��AD���߶�BC�ཻ�ڵ�P����=a�� =b��=k��
��1����ͼ1����a=��b=1ʱ�������k��ֵ��
��2����a=��b=1ʱ(��ͼ2)�������k��ֵ����a=��b=ʱ��k=����
��3����������̽���о����������������⣺����ֱ��д���ú�a��b����ʽ��ʾk=������ ����A(8,0)����B��0��6����C����2��0����ֱ��ADΪ��y=��x+4����k=����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012���㽭ʡ�����п���ѧģ���Ծ����ߣ��������棩 ���ͣ������
 =a��
=a�� =b��
=b�� =k��
=k�� ��b=1ʱ�������k��ֵ��
��b=1ʱ�������k��ֵ�� ��b=1ʱ����ͼ2���������k��ֵ����a=
��b=1ʱ����ͼ2���������k��ֵ����a= ��b=
��b= ʱ��k=______��
ʱ��k=______�� x+4����k=______��
x+4����k=______��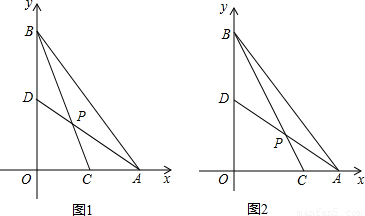
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012ѧ���㽭�������������ѧ�п�ģ����ѧ�Ծ��������棩 ���ͣ������
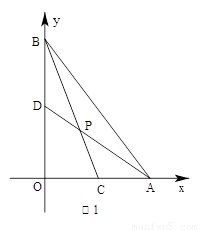
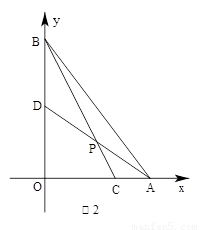
��֪����A��B�ֱ���ֱ������ϵ��x��y����������ϣ�O������ԭ�㣬��C������AO�ϣ���D���߶�OB�ϣ�ֱ��AD���߶�BC�ཻ�ڵ�P����=a�� =b��=k��
��1����ͼ1����a=��b=1ʱ�������k��ֵ��
��2����a=��b=1ʱ(��ͼ2)�������k��ֵ����a=��b=ʱ��k= ����
��3����������̽���о����������������⣺����ֱ��д���ú�a��b����ʽ��ʾk=������ ����A(8,0)����B��0��6����C����2��0����ֱ��ADΪ��y=��x+4����k=����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com