
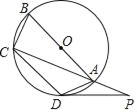
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
(1)若AB=4,求![]() 的长;
的长;
(2)若![]() =
=![]() ,AD=AP,求证:PD是⊙O的切线.
,AD=AP,求证:PD是⊙O的切线.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)连接OC,OD,由圆周角定理得到∠COD=2∠CAD,∠CAD=45°,可得∠COD=90°,根据弧长公式计算即可得到结论;
(2)由已知条件得到∠BOC=∠AOD,由圆周角定理得到∠AOD=45°,根据等腰三角形的性质得到∠ODA=∠OAD=67.5°,利用角和角的关系,求得ADP=![]() ∠CAD=22.5°,得到∠ODP=∠ODA+∠ADP=90°,于是得到结论.
∠CAD=22.5°,得到∠ODP=∠ODA+∠ADP=90°,于是得到结论.
解:
(1)连接OC,OD,
∵∠COD=2∠CAD,∠CAD=45°,
∴∠COD=90°,
∵AB=4,
∴OC=![]() AB=2,
AB=2,
∴![]() 的长=
的长=![]() ×π×2=π;
×π×2=π;
(2)∵![]() =
=![]() ,
,
∴∠BOC=∠AOD,
∵∠COD=90°,
∴∠AOD=45°,
∵OA=OD,
∴∠ODA=∠OAD,
∵∠AOD+∠ODA+∠OAD=180°,
∴∠ODA=67.5°,
∵AD=AP,
∴∠ADP=∠APD,
∵∠CAD=∠ADP+∠APD,∠CAD=45°,
∴∠ADP=![]() ∠CAD=22.5°,
∠CAD=22.5°,
∴∠ODP=∠ODA+∠ADP=90°,
∴PD是⊙O的切线.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】不透明的袋子中装有4个相同的小球,它们除颜色外无其它差别,把它们分别标号:1、2、3、4.
(1)随机摸出一个小球后,放回并摇匀,再随机摸出一个,用列表或画树状图的方法求出“两次取的球标号相同”的概率;
(2)随机摸出两个小球,直接写出“两次取出的球标号和为奇数”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
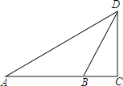
【题目】如图,在△ADC中,∠C=90°,∠A=30°.点B是线段AC上一点,且AB=40cm,∠DBC=75°.
(1)求点B到AD的距离;
(2)求线段CD的长(结果用根号表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,以
,以![]() 为边向外作等边三角形
为边向外作等边三角形![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .则正确的结论是_____.(填序号)
.则正确的结论是_____.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
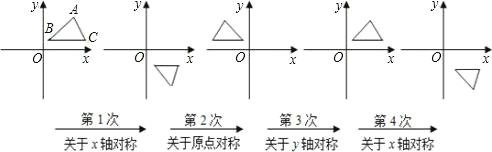
【题目】如图,在平面直角坐标系中,对△ABC 进行循环往复的轴对称或中心对称变换,若原来点 A 坐标是(a,b),则经过第 2012 次变换后所得的 A 点坐标是( )
A. (a,b) B. (a,﹣b) C. (﹣a,b) D. (﹣a,﹣b)
查看答案和解析>>
科目:初中数学 来源: 题型:
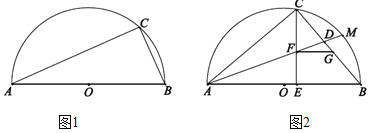
【题目】已知AB是半圆O的直径,点C在半圆O上.
(1)如图1,若AC=3,∠CAB=30°,求半圆O的半径;
(2)如图2,M是![]() 的中点,E是直径AB上一点,AM分别交CE,BC于点F,D. 过点F作FG∥AB交边BC于点G,若△ACE与△CEB相似,请探究以点D为圆心,GB长为半径的⊙D与直线AC的位置关系,并说明理由.
的中点,E是直径AB上一点,AM分别交CE,BC于点F,D. 过点F作FG∥AB交边BC于点G,若△ACE与△CEB相似,请探究以点D为圆心,GB长为半径的⊙D与直线AC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
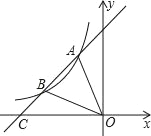
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x<0)的图象相交于点A、点B,与X轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(x<0)的图象相交于点A、点B,与X轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(1)填空:m= ,n= .
(2)求一次函数的解析式和△AOB的面积.
(3)根据图象回答:当x为何值时,kx+b≥![]() (请直接写出答案) .
(请直接写出答案) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )

A. 56° B. 62° C. 68° D. 78°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com