
【题目】如图,![]() 是
是![]() 中
中![]() 边上的中线,过点
边上的中线,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 为
为![]() 外一点,连接
外一点,连接![]() ,且
,且![]() .求证:
.求证:
(1)![]() ;
;
(2)CA平分![]() .
.
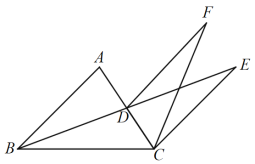
【答案】(1)见解析;(2)见解析
【解析】
(1)根据中线得AD=DC,根据平行线得∠A=∠DCE,∠ABD=∠E,进而根据“AAS”即可得证;
(2)由(1)可得BD=DE,结合DE=DF可得BD=DF,根据等角的补角相等可得∠CDF=∠CDB,进而根据“SAS”可得△CDF≌△CDB,进而得到∠DCF=∠DCB即可得证.
证明:(1)∵BD是△ABC的中线,
∴AD=DC,
∵CE∥AB,
∴∠A=∠DCE,∠ABD=∠E,
在△ABD与△CED中,
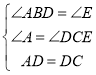
∴△ABD≌△CED(AAS),
(2)∵△ABD≌△CED,
∴BD=DE,
∵DE=DF,
∴BD=DF,
∵∠ADF=∠CDE,∠ADF+∠CDF=180°,∠CDE+∠CDB=180°,
∴∠CDF=∠CDB,
在△CDF与△CDB中,
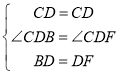
∴△CDF≌△CDB(AAS),
∴∠DCF=∠DCB,
∴CA平分∠BCF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知A,B是抛物线y=ax2(a>0)上两个不同的点,其中A在第二象限,B在第一象限.
(1)如图1所示,当直线AB与x轴平行,∠AOB=90°,且AB=2时,求此抛物线的解析式和A,B两点的横坐标的乘积;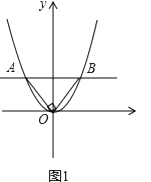
(2)如图2所示,在(1)所求得的抛物线上,当直线AB与x轴不平行,∠AOB仍为90°时,求证:A、B两点横坐标的乘积是一个定值;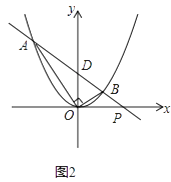
(3)在(2)的条件下,如果直线AB与x轴、y轴分别交于点P、D,且点B的横坐标为 ![]() .那么在x轴上是否存在一点Q,使△QDP为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
.那么在x轴上是否存在一点Q,使△QDP为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张如图1的长方形铁皮,四个角都剪去边长为![]() 的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是
的正方形,再四周折起,做成一个有底无盖的铁盒如图2,铁盒底面长方形的长是![]() ,宽是
,宽是![]() 这个无盖铁盒各个面的面积之和称为铁盒的全面积.
这个无盖铁盒各个面的面积之和称为铁盒的全面积.

(1)图1中原长方形铁皮的面积为_![]() ;(用
;(用![]() 的代数式表示)
的代数式表示)
(2)若要在铁盒的各个外表面漆上某种油漆,每元钱可涂的面积为![]() ,则涂完这个铁盒需要多少钱?(用
,则涂完这个铁盒需要多少钱?(用![]() 的代数式表示)
的代数式表示)
(3)是否存在一个最大正整数![]() ,使得铁盒的全面积是底面积的正整数倍?若存在,请直接写出这个
,使得铁盒的全面积是底面积的正整数倍?若存在,请直接写出这个![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川南充3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是【 】

A.12 B. 24 C. 12![]() D. 16
D. 16![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两张宽度相等的矩形叠放在一起得到如图所示的四边形ABCD,则四边形ABCD是___________形,若两张矩形纸片的长都是10,宽都是4,那么四边形ABCD周长的最大值=___________.
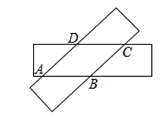
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点D是等边△ABC的边BC上一点,以AD为边向右作等边△ADF,DF与AC交于点N.
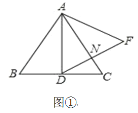
(1)如图①,当AD⊥BC时,请说明DF⊥AC的理由;
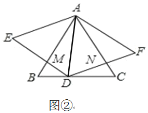
(2)如图②,当点D在BC上移动时,以AD为边再向左作等边△ADE,DE与AB交于点M,试问线段AM和AN有什么数量关系?请说明你的理由;
(3)在(2)的基础上,若等边△ABC的边长为2,直接写出DM+DN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC=CA,∠A=∠ABC=∠ACB,在△ABC的顶点A,C处各有一只小蚂蚁,它们同时出发,分别以相同速度由A向B和由C向A爬行,经过t(s)后,它们分别爬行到了D,E处,设DC与BE的交点为F.
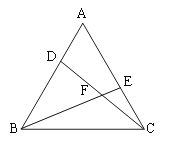
(1)△ACD≌△CBE吗?为什么?
(2)小蚂蚁在爬行过程中,DC与BE所成的∠BFC的大小有无变化?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com