
【题目】如图,在![]() 中,
中,![]() ,分别以
,分别以![]() 的边向外作正方形,连接EC、BF,过B作
的边向外作正方形,连接EC、BF,过B作![]() 于M,交AC于N,下列结论:
于M,交AC于N,下列结论:
![]() ≌
≌![]() ;
;![]() ;
;![]() ;
;![]() ,其中正确的是
,其中正确的是![]()

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
利用全等三角形的判定和性质、平行线的性质、等高模型即可一一判断;
连接BE,AM.
∵AB=AE,AF=AC,∠EAB=∠CAF,
∴∠BAF=∠EAC,
∴△BAF≌△EAC(SAS),故①正确,
∵AE∥CD,
∴S△AEC=S△ABE,
∵S正方形ABDE=2S△ABE,
∴S四边形ABDE=2S△AEC;故②正确;
∵BM⊥FG,AF⊥FG,
∴AF∥BM,
∴S矩形AFMN=2S△AFM=2S△AFB,故③正确,
∵∠ABC=∠ANB=90°,∠BAN=∠BAC,
∴△ABN∽△ACB,
∴AB2=ANAC,
∵AF=AC,
∴AB2=ANAF,
∴S正方形ABDE=S四边形AFMN,故④正确,
故选:D.


科目:初中数学 来源: 题型:
【题目】某年级共有150名女生,为了解该年级女生实心球成绩(单位:米)和一分钟仰卧起坐成绩(单位:个)的情况,从中随机抽取30名女生进行测试,获得了他们的相关成绩,并对数据进行整理、描述和分析.下面给出了部分信息.
a. 实心球成绩的频数分布表如下:
分组 |
|
|
|
|
|
|
频数 | 2 | m | 10 | 6 | 2 | 1 |
b. 实心球成绩在![]() 这一组的是:
这一组的是:
a7.0 7.0 7.0 7.1 7.1 7.1 7.2 7.2 7.3 7.3
c. 一分钟仰卧起坐成绩如下图所示:
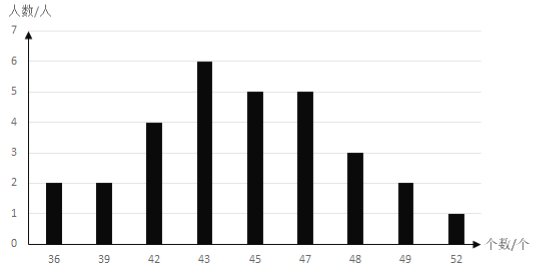
根据以上信息,回答下列问题:
(1) ①表中m的值为__________;
②一分钟仰卧起坐成绩的中位数为__________;
(2)若实心球成绩达到7.2米及以上时,成绩记为优秀.
①请估计全年级女生实心球成绩达到优秀的人数;
②该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如下:
女生代码 | A | B | C | D | E | F | G | H |
实心球 | 8.1 | 7.7 | 7.5 | 7.5 | 7.3 | 7.2 | 7.0 | 6.5 |
一分钟仰卧起坐 | * | 42 | 47 | * | 47 | 52 | * | 49 |
其中有3名女生的一分钟仰卧起坐成绩未抄录完整,但老师说这8名女生中恰好有4人两项测试成绩都达到了优秀,于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀,你同意体育委员的说法吗?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
八(1) | 85 | b | c | 22.8 |
八(2) | a | 85 | 85 | 19.2 |
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=ax2+bx+c(其中a,b,c为常数,且a≠0),乐老师在用描点法画其的图象时,列出如下表格,根据该表格,下列判断中不正确的是( )
x | … | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣2 | 2.5 | 4 | 2.5 | … |
A. a<0
B. 一元二次方程ax2+bx+c﹣5=0没有实数根
C. 当x=3时y=﹣2
D. 一元二次方程ax2+bx+c=0有一根比3大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中有完全相同的三个小球,把它们分别标号为1,2,3. 小林和小华做一个游戏,按照以下方式抽取小球:先从布袋中随机抽取一个小球,记下标号后放回布袋中搅匀,再从布袋中随机抽取一个小球, 记下标号. 若两次抽取的小球标号之和为奇数,小林赢;若标号之和为偶数,则小华赢.
(1)用画树状图或列表的方法,列出前后两次取出小球上所标数字的所有可能情况;
(2)请判断这个游戏是否公平,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的一种产品按照质量由高到低分为A,B,C,D四级,为了增加产量、提高质量,该公司改进了一次生产工艺,使得生产总量增加了一倍.为了解新生产工艺的效果,对改进生产工艺前、后的四级产品的占比情况进行了统计,绘制了如下扇形图:
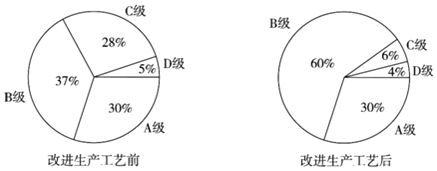
根据以上信息,下列推断合理的是( )
A.改进生产工艺后,A级产品的数量没有变化
B.改进生产工艺后,B级产品的数量增加了不到一倍
C.改进生产工艺后,C级产品的数量减少
D.改进生产工艺后,D级产品的数量减少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某部门为新的生产线研发了一款机器人,为了了解它的操作技能情况,在相同条件下与人工操作进行了抽样对比.过程如下,请补充完整.
收集数据对同一个生产动作,机器人和人工各操作20次,测试成绩(十分制)如下:
机器人 | 8.0 | 8.1 | 8.1 | 8.1 | 8.2 | 8.2 | 8.3 | 8.4 | 8.4 | 9.0 |
9.0 | 9.0 | 9.1 | 9.1 | 9.4 | 9.5 | 9.5 | 9.5 | 9.5 | 9.6 | |
人工 | 6.1 | 6.2 | 6.6 | 7.2 | 7.2 | 7.5 | 8.0 | 8.2 | 8.3 | 8.5 |
9.1 | 9.6 | 9.8 | 9.9 | 9.9 | 9.9 | 10 | 10 | 10 | 10 |
整理、描述数据按如下分段整理、描述这两组样本数据:
成绩x 人数 生产方式 | 6≤x<7 | 7≤x<8 | 8≤x<9 | 9≤x≤10 |
机器人 | 0 | 0 | 9 | 11 |
人工 |
|
|
|
(说明:成绩在9.0分及以上为操作技能优秀,8.0~8.9分为操作技能良好,6.0~7.9分为操作技能合格,6.0分以下为操作技能不合格)
分析数据两组样本数据的平均数、中位数、众数和方差如下表所示:
平均数 | 中位数 | 众数 | 方差 | |
机器人 | 8.8 | 9.0 | 9.5 | 0.333 |
人工 | 8.6 | 8.8 | 10 | 1.868 |
得出结论
(1)如果生产出一个产品,需要完成同样的操作200次,估计机器人生产这个产品达到操作技能优秀的次数为 ;
(2)请结合数据分析机器人和人工在操作技能方面各自的优势: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.
(1)若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 ;
(2)若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=x﹣2与双曲线y=![]() (k≠0)相交于A,B两点,且点A的横坐标是3.
(k≠0)相交于A,B两点,且点A的横坐标是3.
(1)求k的值;
(2)过点P(0,n)作直线,使直线与x轴平行,直线与直线y=x﹣2交于点M,与双曲线y=![]() (k≠0)交于点N,若点M在N右边,求n的取值范围.
(k≠0)交于点N,若点M在N右边,求n的取值范围.
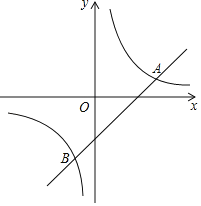
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com