
【题目】如图,抛物线![]() 的对称轴是
的对称轴是![]() ,下列结论:
,下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .
.
其中正确的结论有________(填上正确结论的序号).

【答案】①②④
【解析】
由函数的图象得出抛物线开口向上,与x轴有两个交点,与y轴交点在负半轴上,且对称轴为x=1,且x=1或x=2时对应的函数值小于0,x=1或x=3时对应的函数值大于0,进而确定出b2﹣4ac大于0,选项①正确;a大于0,a与b异号,c小于0,根据对称轴公式得出a与b的关系式2a+b=0,由c<0,在不等式左右两边同时加上﹣b,将右边的﹣b化为2a,变形后得到不等式,可得出④正确;由抛物线图象及对称性得到x=3时,所对应的函数值y大于0,将x=3代入抛物线解析式后,将表示出的a代入,可得出3b小于2c,选项②正确;将x=1代入抛物线解析式得到a+b+c小于0,再将x=﹣1代入抛物线解析式得到a﹣b+c大于0,两个不等式相乘,根据两数相乘异号得负的取符号法则及平方差公式变形后,得到(a+c)2小于b2,选项③错误;由x=2时对应的函数值小于0,将x=2代入抛物线解析式中得到4a+2b+c小于0,选项⑤错误,即可确定出正确选项的序号.
由函数图象可得:抛物线开口向上,与y轴交点在y轴负半轴,抛物线与x轴有两个交点,∴a>0,c<0,b2﹣4ac>0,选项①正确;
又抛物线的对称轴为直线x=﹣![]() =1,∴2a+b=0,即b=﹣2a,∴b<0.
=1,∴2a+b=0,即b=﹣2a,∴b<0.
∵x=3时,y=9a+3b+c>0,且a=﹣![]() b,∴﹣
b,∴﹣![]() b+3b+c>0,即c>
b+3b+c>0,即c>![]() b,∴3b<2c,选项②正确;
b,∴3b<2c,选项②正确;
∵x=1时,y=a+b+c<0,x=﹣1时,y=a﹣b+c>0,∴(a+b+c)(a﹣b+c)<0,即[(a+c)+b][(a+c)﹣b]=(a+c)2﹣b2<0,∴(a+c)2<b2,选项③错误;
∵c<0,∴﹣b+c<﹣b,又b=﹣2a,∴﹣b+c<2a,即a>![]() ,选项④正确;
,选项④正确;
∵x=2时,y=4a+2b+c<0,选项⑤错误,则正确的序号有:①②④.
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】某篮球架的侧面示意图如图所示,现测得如下数据:底部支架AB的长为1.74m,后拉杆AE的倾斜角∠EAB=53°,篮板MN到立柱BC的水平距离BH=1.74m,在篮板MN另一侧,与篮球架横伸臂DG等高度处安装篮筐,已知篮筐到地面的距离GH的标准高度为3.05m.则篮球架横伸臂DG的长约为_____m(结果保留一位小数,参考数据:sin53°≈![]() , cos53°≈
, cos53°≈![]() ,tan53°≈
,tan53°≈![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AB上,CD=CB,点E为BD的中点,且EA=EC,点F为AC的中点,连接EF交CD于点M,连接AM.
(1)求证:EF=![]() AC;
AC;
(2)求线段AM、DM、BC之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,现有边长为1,a(a>1)的一张矩形纸片ABCD,把这个矩形按要求分割,画出分割线,并在相应的位置上写出a的值.
(1)把这个矩形分成两个全等的小矩形,且分成的两个矩形与原矩形相似.
(2)把这个和矩形分成三个矩形,且每一个矩形都与原矩形相似,给出两种不同的分割.

查看答案和解析>>
科目:初中数学 来源: 题型:
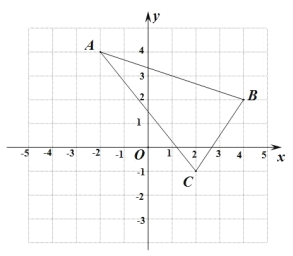
【题目】如图,△ABC 在平面直角坐标系中,点 A,B,C 的坐标分别为 A(-2,4),B(4,2),C(2,-1).
(Ⅰ)请在平面直角坐标系内,画出△ABC 关于 x 轴的对称图形△A1B1C1,其中,点 A,B,C 的对应点分别为A1,B1,C1;
(Ⅱ)请写出点C(2,-1)关于直线m(直线m上格点的横坐标都为-1)对称的点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用我们学过的知识,可以得出下面这个优美的等式:
![]() ;该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
;该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
⑴.请你证明这个等式;
⑵.如果![]() ,请你求出
,请你求出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知平面内一点![]() 与一直线
与一直线![]() ,如果过点
,如果过点![]() 作直线
作直线![]() ,垂足为
,垂足为![]() ,那么垂足
,那么垂足![]() 叫做点
叫做点![]() 在直线
在直线![]() 上的射影;如果线段
上的射影;如果线段![]() 的两个端点
的两个端点![]() 和
和![]() 在直线
在直线![]() 上的射影分别为点
上的射影分别为点![]() 和
和![]() ,那么线段
,那么线段![]() 叫做线段
叫做线段![]() 在直线
在直线![]() 上的射影.
上的射影.
如图①,已知平面内一点![]() 与一直线
与一直线![]() ,如果过点
,如果过点![]() 作直线
作直线![]() ,垂足为
,垂足为![]() ,那么垂足
,那么垂足![]() 叫做点
叫做点![]() 在直线
在直线![]() 上的射影;如果线段
上的射影;如果线段![]() 的两个端点
的两个端点![]() 和
和![]() 在直线
在直线![]() 上的射影分别为点
上的射影分别为点![]() 和
和![]() ,那么线段
,那么线段![]() 叫做线段
叫做线段![]() 在直线
在直线![]() 上的射影.
上的射影.
![]() 如图②,
如图②,![]() 、
、![]() 为线段
为线段![]() 外两点,
外两点,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .
.
则![]() 点在
点在![]() 上的射影是________点,
上的射影是________点,![]() 点在
点在![]() 上的射影是________点,
上的射影是________点,
线段![]() 在
在![]() 上的射影是________,线段
上的射影是________,线段![]() 在
在![]() 上的射影是________;
上的射影是________;
![]() 根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com