分析:(1)首先连接O
1D,由FC是⊙O
1的切线,AC是⊙O
2的直径,即可证得AF∥O
1D,又由O
1A=O
1D,易证得∠FAD=∠DAC,然后由同圆或等圆中,同弧所对的圆周角相等,即可证得△AEF∽△ACD,根据相似三角形的对应边成比例,即可证得AC•AF=AD•AE;
(2)首先连接EC,由AB是⊙O
1的直径,AC是⊙O
2的直径,可得
==,又由⊙O
1与⊙O
2内切,O
1O
2=9,可得AC-AB=18,然后由DE=AE-AD=
AC-
AD求得答案.
解答:(1)证明:连接O
1D,
∵FC是⊙O
1的切线,
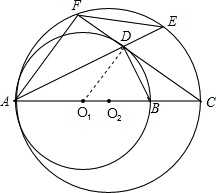
∴O
1D⊥FC,
∴AC是⊙O
2的直径,
∴∠AFC=90°,
∴AF⊥FC,
∴AF∥O
1D,
∴∠FAD=∠AD0
1,
∵O
1A=O
1D,
∴∠O
1AD=O
1DA,
∴∠FAD=∠DAC,
∵∠E=∠C,
∴△AEF∽△ACD,
∴
=,
∴AC•AF=AD•AE;
(2)解:连接EC,
∵AB是⊙O
1的直径,AC是⊙O
2的直径,
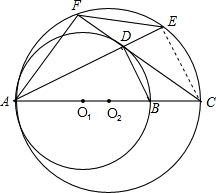
∴∠ADB=∠AEC=90°,
∵cos∠BAD=
,
∴
==,
∴AD=
AB,AE=
AC,
∵⊙O
1与⊙O
2内切,O
1O
2=9,
∴0
2A-O
1A=9,
∴AC-AB=18,
∴DE=AE-AD=
AC-
AD=
(AC-AD)=
×18=12.
点评:此题考查了圆的切线的性质,两圆内切的性质以及相似三角形的判定与性质等知识.此题难度较大,解题的关键是注意辅助线的作法,注意数形结合思想与转化思想的应用.

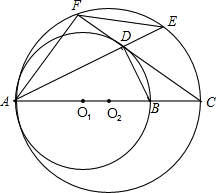 O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.
O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.



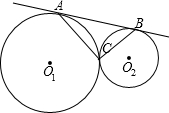 已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=
已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=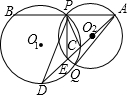 (1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且
(1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且