
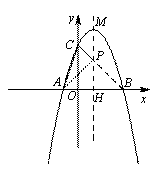
如图,已知抛物线![]() 与
与![]() 轴交于A(-1,0)、B(3,0)两点,与
轴交于A(-1,0)、B(3,0)两点,与![]() 轴交于点C(0,3).
轴交于点C(0,3).
(1)求抛物线的解析式及顶点M坐标;
(2)在抛物线的对称轴上找到点P,使得△PAC的周长最小,并求出点P的坐标;
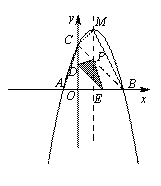
(3)若点D是线段OC上的一个动点(不与点O、C重合).过点D作DE∥PC交![]() 轴于点E.设CD的长为m,问当m取何值时,S△PDE =
轴于点E.设CD的长为m,问当m取何值时,S△PDE =![]() S四边形ABMC.
S四边形ABMC.

解:(1)∵ 抛物线![]() (
(![]() )A(-1,0)、B(3,0)C(0,3)三点,
)A(-1,0)、B(3,0)C(0,3)三点,
 ∴
∴ ![]() ,解得
,解得 ![]() .
.
∴ 抛物线的解析式为![]() ,顶点M为(1,4).
,顶点M为(1,4).
(2)∵ 点A、B关于抛物线的对称轴对称,
∴ 连结BC与抛物线对称轴交于一点,即为所求点P.
设对称轴与x轴交于点H,
∵ PH∥y轴,
∴ △PHB∽△CBO.
∴ ![]() .
.
由题意得BH=2,CO=3,BO=3,
 ∴ PH=2.
∴ PH=2.
∴ P(1,2).
(3)∵ A(-1,0)B(3,0),C(0,3),M(1,4),
∴ S四边形ABMC=9.
∵ S四边形ABMC =9S△PDE, ∴![]() =1.
=1.
∵ OC=OD,∴∠OCB=∠OBC= 45°.
∵ DE∥PC,∴∠ODE=∠OED= 45°.
∴ OD=OE=3-m.
∵ S四边形PDOE=![]() ,
,
∴ S△PDE= S四边形PDOE- S△DOE=![]() (0<m<3).
(0<m<3).
∴![]() .解得,m1=1, m2=2.
.解得,m1=1, m2=2.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
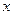 轴交于点
轴交于点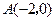 ,
,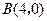 ,与
,与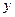 轴交于点
轴交于点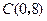 .
.
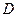 的坐标;
的坐标;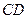 交
交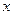 轴于点
轴于点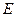 .在线段
.在线段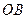 的垂直平分线上是否存在点
的垂直平分线上是否存在点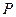 ,使得点
,使得点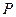 到直线
到直线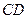 的距离等于点
的距离等于点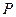 到原点
到原点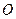 的距离?如果存在,求出点
的距离?如果存在,求出点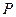 的坐标;如果不存在,请说明理由;
的坐标;如果不存在,请说明理由;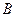 作
作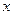 轴的垂线,交直线
轴的垂线,交直线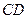 于点
于点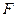 ,将抛物线沿其对称轴平移,使抛物线与线段
,将抛物线沿其对称轴平移,使抛物线与线段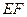 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?查看答案和解析>>
科目:初中数学 来源: 题型:
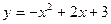 与
与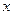 轴的两个交点为A、B,与
轴的两个交点为A、B,与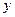 轴交于点C
轴交于点C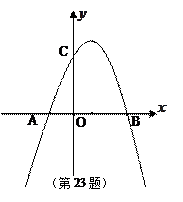
查看答案和解析>>
科目:初中数学 来源:2011年陕西省西安音乐学院初一上学期期末考试数学卷 题型:解答题
如图,已知抛物线与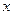 轴交于点
轴交于点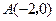 ,
,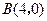 ,与y轴交于点
,与y轴交于点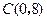 .
.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交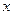 轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源:2011年陕西省西安音乐学院初一上学期期末考试数学卷 题型:解答题
如图,已知抛物线与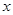 轴交于点
轴交于点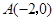 ,
,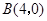 ,与y轴交于点
,与y轴交于点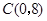 .
.

(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交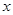 轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源:2010年湖北省黄冈市初二上学期期末数学卷 题型:解答题
如图,已知抛物线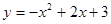 与
与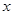 轴的两个交点为A、B,与
轴的两个交点为A、B,与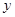 轴交于点C
轴交于点C
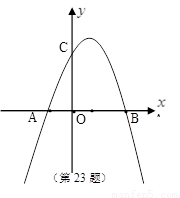
(1)求A、B、C三点的坐标?
(2)用配方法求该二次函数的对称轴和顶点坐标?
(3)若坐标平面内的点M,使得以点M和三点A、B、C为顶点的四边形是平行四边形,求点M的坐标?(直接写出M的坐标,不用说明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com