
分析 (1)根据给定钝角的三角函数值,代入数据,即可求出结论;
(2)根据三角形的内角和定理以及三个角的比例可得出三角形的三个内角,分①A=B=30°;②A=30°、B=120°;③A=120°、B=30°.三种情况考虑,根据特殊角的三角函数值找出sinA、cosB的值,再根据根与系数的关系找出关于a、b的二元一次方程组,解方程组即可得出结论.
解答 解:(1)sin120°=sin(180°-120°)=sin60°=$\frac{3}{2}$;
cos135°=-cos(180°-135°)=-cos45°=-$\frac{\sqrt{2}}{2}$;
tan150°=-tan(180°-150°)=-tan30°=-$\frac{\sqrt{3}}{3}$.
(2)∵一个三角形的三个内角的比是1:1:4,且三角形的内角和为180°,
∴三角形的三个内角为30、30、120.
①当A=30°、B=30°时,sinA=$\frac{1}{2}$,cosB=$\frac{\sqrt{3}}{2}$,
∵sinA,cosB是方程ax2-bx-1=0的两个不相等的实数根,
∴$\left\{\begin{array}{l}{\frac{1}{2}+\frac{\sqrt{3}}{2}=\frac{b}{a}}\\{\frac{1}{2}×\frac{\sqrt{3}}{2}=-\frac{1}{a}}\end{array}\right.$,
解得:a=-$\frac{4\sqrt{3}}{3}$,b=-2-$\frac{2\sqrt{3}}{3}$;
②当A=30°、B=120°时,sinA=$\frac{1}{2}$,cosB=-$\frac{1}{2}$,
∵sinA,cosB是方程ax2-bx-1=0的两个不相等的实数根,
∴$\left\{\begin{array}{l}{\frac{1}{2}-\frac{1}{2}=\frac{b}{a}}\\{\frac{1}{2}×(-\frac{1}{2})=-\frac{1}{a}}\end{array}\right.$,
解得:a=4,b=0;
③当A=120°、B=30°时,sinA=$\frac{\sqrt{3}}{2}$,cosB=$\frac{\sqrt{3}}{2}$,
此时sinA=cosB,不满足题意.
综上可知:当A=B=30°时,a=-$\frac{4\sqrt{3}}{3}$,b=-2-$\frac{2\sqrt{3}}{3}$;当A=30°、B=120°时,a=4,b=0.
点评 本题考查了特殊角的三角函数值、三角形内角和定理以及根与系数的关系,熟练掌握特殊角的三级函数值是解题的关键.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
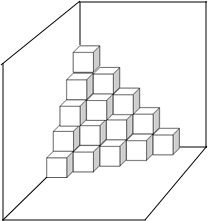 如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层…
如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层…查看答案和解析>>
科目:初中数学 来源: 题型:选择题
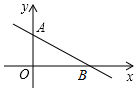 平面直角坐标系中,直线y=-$\frac{1}{2}$x+2和x、y轴交于A、B两点,在第二象限内找一点P,使△PAO和△AOB相似的三角形个数为( )
平面直角坐标系中,直线y=-$\frac{1}{2}$x+2和x、y轴交于A、B两点,在第二象限内找一点P,使△PAO和△AOB相似的三角形个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
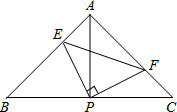 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
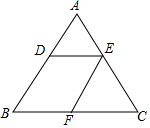 已知:如图,△ABC中,DE∥BC.
已知:如图,△ABC中,DE∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com