
分析 首先对括号内的分式进行通分相加,把除法转化为乘法,计算乘法即可化简,然后代入x的值计算即可.
解答 解:原式=$\frac{2x-1-(x+1)(x-1)}{x+1}$•$\frac{(x+1)^{2}}{x-2}$
=-$\frac{{x}^{2}-2x}{x+1}$•$\frac{(x+1)^{2}}{x-2}$
=-x(x+1),
当x=-$\frac{1}{3}$时,原式=$\frac{1}{3}$×(-$\frac{1}{3}$+1)=$\frac{1}{3}$×$\frac{2}{3}$=$\frac{2}{9}$.
点评 本题考查了分式的化简求值,正确进行通分、约分是关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
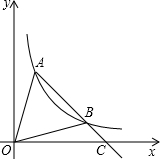 如图,A、B为反比例函数y=$\frac{k}{x}$(x>0)图象上的两点,A、B两点坐标分别为(m,5-m)、(n,5-n)(m<n),连接AB并延长交x轴于点C.
如图,A、B为反比例函数y=$\frac{k}{x}$(x>0)图象上的两点,A、B两点坐标分别为(m,5-m)、(n,5-n)(m<n),连接AB并延长交x轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,Rt△ACB中,∠C=90°,AC=12,BC=5,等腰Rt△DEF的顶点D、E分别在边AC、AB上,且ED⊥AC于点D,连接AF并延长交BC于点G.已知DE=EF=2,则BG的长为( )
如图,Rt△ACB中,∠C=90°,AC=12,BC=5,等腰Rt△DEF的顶点D、E分别在边AC、AB上,且ED⊥AC于点D,连接AF并延长交BC于点G.已知DE=EF=2,则BG的长为( )| A. | $\frac{25}{17}$ | B. | $\frac{30}{17}$ | C. | $\frac{17}{12}$ | D. | $\frac{19}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是( )米.
如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是( )米.| A. | 7 | B. | 11 | C. | 13 | D. | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com