
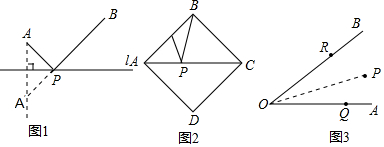
分析 (1)由于点B与D关于AC对称,所以连接DE,与AC的交点即为P点.此时PB+PE=DE最小,而DE是直角△ADB的斜边,由勾股定理可求出结果;
(2)设点P关于OA、OB对称点分别为M、N,当点R、Q在MN上时,△PQR周长为PR+RQ+QP=MN,此时周长最小.
解答 解:(1)如图1,
连接DE,与交于点P.
∵点B与D关于AC对称,
∴DP=BP,
∴PB+PE=PD+PE=DE,
∵在直角△ADE中,∠DAE=90°,AD=2,AE=1,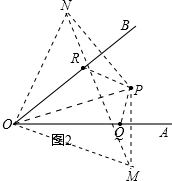
∴DE=$\sqrt{5}$,
(2)分别作点P关于OA、OB的对称点M、N,
连接OM、ON、MN,MN交OA、OB于点Q、R,
连接PR、PQ,此时△PQR周长的最小值等于MN.
由轴对称性质可得,OM=ON=OP=10,∠MOA=∠POA,∠NOB=∠POB,
∴∠MON=2∠AOB=2×45°=90°,
在Rt△MON中,MN=$\sqrt{O{M}^{2}+O{N}^{2}}$=10$\sqrt{2}$.
即△PQR周长的最小值等10$\sqrt{2}$.
点评 此题是四边形综合题,主要考查了正方形的性质,对称的性质,解本题的关键是根据对称的性质画出图形,是一道比较简单的基本题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
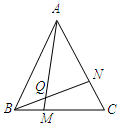 (1)学完全等三角形以后,老师布置了这样一道题:如图,点M、N分别在等边△ABC的BC、CA边上,且BM=CN,AM、BN交于点Q.求证:∠BQM=60°.(注意:等边三角形三条边都相等,每个内角都是60°)
(1)学完全等三角形以后,老师布置了这样一道题:如图,点M、N分别在等边△ABC的BC、CA边上,且BM=CN,AM、BN交于点Q.求证:∠BQM=60°.(注意:等边三角形三条边都相等,每个内角都是60°)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com