
 (a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.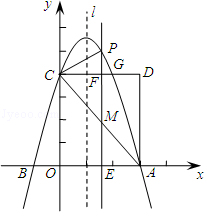
 (a≠0)经过点A(3,0),点C(0,4),
(a≠0)经过点A(3,0),点C(0,4),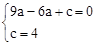 ,解得
,解得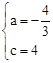 。
。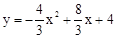 。
。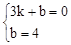 ,解得
,解得 。
。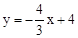 。
。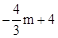 )。
)。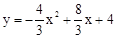 上,
上,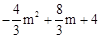 )。
)。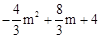 )-(
)-(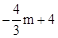 )=
)=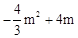 。
。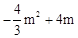 (0<m<3)。
(0<m<3)。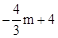 ,CF=m,PF=
,CF=m,PF=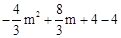 =
= ,
, ):(3-m)=m:(
):(3-m)=m:(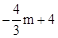 ),
),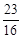 。
。 ):(
):(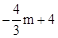 ),
),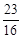 或1,△PCM为直角三角形或等腰三角形。
或1,△PCM为直角三角形或等腰三角形。 ,运用待定系数法即可求出抛物线的解析式。
,运用待定系数法即可求出抛物线的解析式。

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
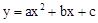 与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).
与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).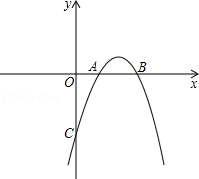
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
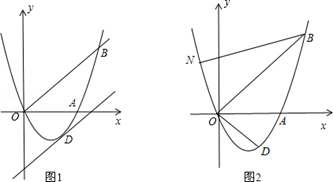
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.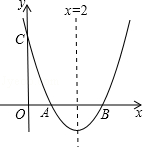
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 .
与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 .
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com