

|
|
| 22+22 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| OQ |
| tan30° |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |


科目:初中数学 来源: 题型:
| 3 |
| 5 |
19±
| ||
| 6 |
19±
| ||
| 6 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
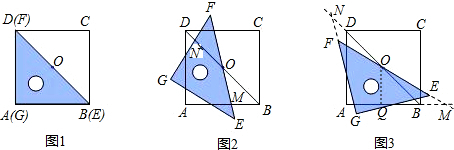
 经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.
经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.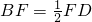 ?(请直接写出答案).
?(请直接写出答案).
查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省永春县九年级上学期期末检测数学试卷(解析版) 题型:选择题
如图,将一张等腰直角三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为直角梯形,乙为等腰直角三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断正确的是( )

A.甲>乙>丙;?? B.乙>丙>甲;?? C.丙>乙>甲;?? D.丙>甲>乙.
查看答案和解析>>
科目:初中数学 来源:2011年浙江省温州市瑞安市中考数学模拟试卷(解析版) 题型:解答题
 经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.
经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源:江苏省期末题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com