
| A. | 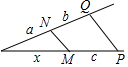 | B. |  | C. | 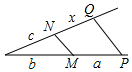 | D. | 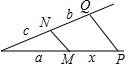 |
分析 根据平行线分线段成比例定理对各个选项进行判断即可.
解答 解:A、∵MN∥PQ,
∴$\frac{x}{c}=\frac{a}{b}$,则x=$\frac{ac}{b}$,故错误;
B、∵MN∥PQ,
∴$\frac{x}{c}=\frac{b}{a}$,则x=$\frac{bc}{a}$,故正确;
C、∵MN∥PQ,
∴$\frac{b}{a}$=$\frac{c}{x}$,则x=$\frac{ac}{b}$,故错误;
D、∵MN∥PQ,
∴$\frac{a}{x}=\frac{c}{b}$,则x=$\frac{ab}{c}$,故错误,
故选:B.
点评 本题考查的是平行线分线段成比例定理,找准对应关系,灵活运用定理是解题的关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
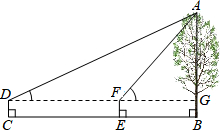 如图,小明同学用仪器测量一棵大树AB的高度,在C处测得∠ADG=30°,在E处测得∠AFG=60°,CE=8米,仪器高度CD=1.4米.
如图,小明同学用仪器测量一棵大树AB的高度,在C处测得∠ADG=30°,在E处测得∠AFG=60°,CE=8米,仪器高度CD=1.4米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com