
 如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),$\widehat{A{A}_{1}}$是以点B为圆心,BA为半径的圆弧,$\widehat{{A}_{1}{A}_{2}}$是以点O为圆心,OA1为半径的圆弧,$\widehat{{A}_{2}{A}_{3}}$是以点C为圆心,CA2为半径的圆弧,$\widehat{{A}_{3}{A}_{4}}$是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心按上述做法得到的曲线AA1A2A3A4A5…称为正方形的渐开线“,那么点A5的坐标是(6,0),点A2016的坐标是(1,2017).
如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),$\widehat{A{A}_{1}}$是以点B为圆心,BA为半径的圆弧,$\widehat{{A}_{1}{A}_{2}}$是以点O为圆心,OA1为半径的圆弧,$\widehat{{A}_{2}{A}_{3}}$是以点C为圆心,CA2为半径的圆弧,$\widehat{{A}_{3}{A}_{4}}$是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心按上述做法得到的曲线AA1A2A3A4A5…称为正方形的渐开线“,那么点A5的坐标是(6,0),点A2016的坐标是(1,2017). 分析 根据画弧的方法以及罗列部分点的坐标发现:点Ax的坐标满足“A4n=(1,4n+1),A4n+1=(4n+2,0),A4n+2=(0,-(4n+2)),A4n+3=(-(4n+3),1)”,根据这一规律即可得出A5和A2016点的坐标.
解答 解:观察,找规律:A(1,1),A1(2,0),A2(0,-2),A3(-3,1),A4(1,5),A5(6,0),A6(0,-6),A7(-7,1),A8(1,9)…,
∴A4n=(1,4n+1),A4n+1=(4n+2,0),A4n+2=(0,-(4n+2)),A4n+3=(-(4n+3),1).
∵5=4+1,2016=504×4,
∴A5的坐标为(64+2,0)=(6,0),A2016的坐标为(1,4×504+1)=(1,2017).
故答案为:(6,0);(1,2017).
点评 本题考查了规律型中的点的坐标,解题的关键是罗列出部分点的坐标找出“A4n=(1,4n+1),A4n+1=(4n+2,0),A4n+2=(0,-(4n+2)),A4n+3=(-(4n+3),1)”这一规律.本题属于基础题,难度不大,解决该题型题目时,结合画弧的方法以及部分点的坐标寻找出来点的排布规律是关键.


科目:初中数学 来源: 题型:选择题
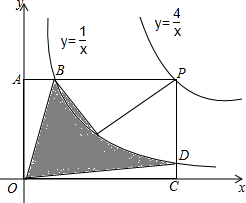 如图,点P为反比例函数y=$\frac{4}{x}$(x>0)图象上一点,过点P作y轴的垂线,交双曲线y=$\frac{1}{x}$于点B,交y轴于点A,过点P作x轴的垂线,交双曲线y=$\frac{1}{x}$于点D,交x轴于点C,连接OP交双曲线y=$\frac{1}{x}$于点E,则连接BO,OD,DE,EB而围成的阴影部分面积为( )
如图,点P为反比例函数y=$\frac{4}{x}$(x>0)图象上一点,过点P作y轴的垂线,交双曲线y=$\frac{1}{x}$于点B,交y轴于点A,过点P作x轴的垂线,交双曲线y=$\frac{1}{x}$于点D,交x轴于点C,连接OP交双曲线y=$\frac{1}{x}$于点E,则连接BO,OD,DE,EB而围成的阴影部分面积为( )| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,AB=AC,点D是BC的中点,AD=AE,AE⊥BE,垂足为E,连结DE.
已知:如图,AB=AC,点D是BC的中点,AD=AE,AE⊥BE,垂足为E,连结DE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
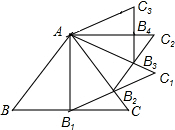 如图,等边△ABC的边长为2,以BC边上的高AB1为边作等边△AB1C1,B1C1交AC于点B2,△AB1B2的面积记做S1;再以AB2为边作等边△AB2C2,B2C2交AC1于点B3,△AB2B3的面积记做S2;…,以此类推,则Sn=$\frac{\sqrt{3}}{2}×(\frac{3}{4})^{n}$..
如图,等边△ABC的边长为2,以BC边上的高AB1为边作等边△AB1C1,B1C1交AC于点B2,△AB1B2的面积记做S1;再以AB2为边作等边△AB2C2,B2C2交AC1于点B3,△AB2B3的面积记做S2;…,以此类推,则Sn=$\frac{\sqrt{3}}{2}×(\frac{3}{4})^{n}$..查看答案和解析>>
科目:初中数学 来源: 题型:填空题
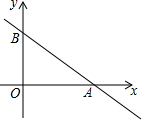 如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
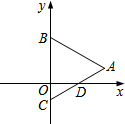 如图,在平面直角坐标系中,点B、C在y轴上,△ABC是等边三角形,AB=4,AC与x轴的交点D的坐标是($\sqrt{3}$,0),则点A的坐标为( )
如图,在平面直角坐标系中,点B、C在y轴上,△ABC是等边三角形,AB=4,AC与x轴的交点D的坐标是($\sqrt{3}$,0),则点A的坐标为( )| A. | (1,2$\sqrt{3}$) | B. | (2,2$\sqrt{3}$) | C. | (2$\sqrt{3}$,1) | D. | (2$\sqrt{3}$,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
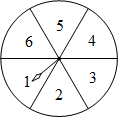 如图,转盘被等分成6个扇形,每个扇形上依次标有数字1,2,3,4,5,6.在游戏中特别规定:当指针指向边界时,重新转动转盘.
如图,转盘被等分成6个扇形,每个扇形上依次标有数字1,2,3,4,5,6.在游戏中特别规定:当指针指向边界时,重新转动转盘.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
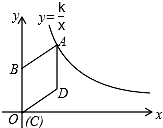 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com