
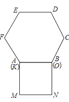
【题目】已知正方形![]() 和正六边形
和正六边形![]() 边长均为1,如图所示,把正方形放置在正六边形外,使
边长均为1,如图所示,把正方形放置在正六边形外,使![]() 边与
边与![]() 边重合,按下列步骤操作:将正方形在正六边形外绕点
边重合,按下列步骤操作:将正方形在正六边形外绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 边与
边与![]() 边重合,完成第一次旋转;再绕点
边重合,完成第一次旋转;再绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 边与
边与![]() 边重合,完成第二次旋转;此时点
边重合,完成第二次旋转;此时点![]() 经过路径的长为___________.若按此方式旋转,共完成六次,在这个过程中点
经过路径的长为___________.若按此方式旋转,共完成六次,在这个过程中点![]() ,
,![]() 之间距离的最大值是______.
之间距离的最大值是______.
 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】某服装店用36000元购进进价为1200元/件的甲品牌的服装和进价为1000元/件的乙品牌的服装,销售完后共获利6000元,其中甲品牌的服装每件售件为1380元,乙品牌的服装每件售件为1200元.
(1)该服装店购进甲、乙两种服装各多少件?
(2)该服装店销售完甲乙两种服装后,第二次又以原价购进甲,乙两种服装,购进乙种服装的件数不变,购进甲服装的件数是第一次的2倍,甲种服装按原价出售,而乙种服装打折销售;若两种服装销售完毕,要使第二次销售活动获利不少于8160元,则乙种服装最低打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形的边长均为1,线段AB、线段EF的端点均在小正方形的顶点上.
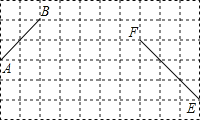
(1)在图中以AB为边画Rt△BAC,点C在小正方形的顶点上,使∠BAC=90°,tan∠ACB=![]() ;
;
(2)在(1)的条件下,在图中画以EF为边且面积为3的△DEF,点D在小正方形的顶点上,连接CD、BD,使△BDC是锐角等腰三角形,直接写出∠DBC的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以固定进价一次性购进一种商品,7月份按一定售价销售,销售额为120000元,为扩大销量,减少库存,8月份在7月份售价基础上打8折销售,结果销售量增加40件,销售额增加8000元.
(1)求该商店7月份这种商品的售价是多少元?
(2)如果该商品的进价为750元,那么该商店7月份销售这种商品的利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() 和点
和点![]() ,点
,点![]() 在点
在点![]() 的右侧,点
的右侧,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 沿
沿![]() 轴的正方向平移
轴的正方向平移![]() 个单位后得到线段
个单位后得到线段![]() .
.
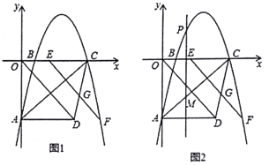
(1)当![]() ______时,点
______时,点![]() 或点
或点![]() 正好移动到抛物线上;
正好移动到抛物线上;
(2)当点![]() 正好移动到抛物线上,
正好移动到抛物线上,![]() 与
与![]() 相交于点
相交于点![]() 时,求
时,求![]() 点坐标;
点坐标;
(3)如图2,若点![]() 是
是![]() 轴上方抛物线上一动点,过点
轴上方抛物线上一动点,过点![]() 作平行于
作平行于![]() 轴的直线交
轴的直线交![]() 于点
于点![]() ,探索是否存在点
,探索是否存在点![]() ,使线段
,使线段![]() 长度有最大值?若存在,直接写出点
长度有最大值?若存在,直接写出点![]() 的坐标和
的坐标和![]() 长度的最大值;若不存在,请说明理由.
长度的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
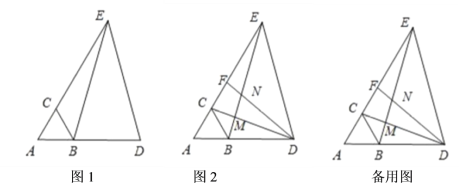
【题目】如图,在等边![]() 中,延长
中,延长![]() 至点
至点![]() ,延长
,延长![]() 交
交![]() 的中垂线于点
的中垂线于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图1,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)如图2,连接![]() 交
交![]() 于点
于点![]() ,在
,在![]() 上取一点
上取一点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,若![]() 直接写出线段
直接写出线段![]() ,
,![]() ,
,![]() 的等量关系
的等量关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线G:![]() 与
与![]() 轴交于点C,抛物线G的顶点为D,直线
轴交于点C,抛物线G的顶点为D,直线![]() :
:![]() .
.
(1)当![]() 时,直接写出直线
时,直接写出直线![]() 被抛物线G截得的线段长;
被抛物线G截得的线段长;
(2)随着![]() 取值的变化,判断点C,D是否都在直线
取值的变化,判断点C,D是否都在直线![]() 上;
上;
(3)若直线被![]() 被抛物线G截得的线段长不小于
被抛物线G截得的线段长不小于![]() ,结合函数图像,直接写出m的取值范围.
,结合函数图像,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB⊥x轴于点E,正比例函数y=mx的图像与反比例函数![]() 的图像交于A,P两点.
的图像交于A,P两点.
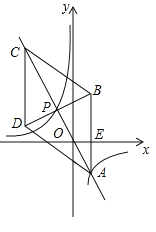
(1)求m,n的值与点A的坐标
(2)求![]() 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com