
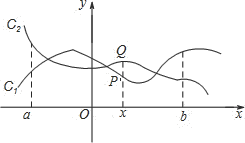
【题目】如图,点![]() 与
与![]() 分别是两个函数图象
分别是两个函数图象![]() 与
与![]() 上的任一点.当
上的任一点.当![]() 时,有
时,有![]() 成立,则称这两个函数在
成立,则称这两个函数在![]() 上是“相邻函数”,否则称它们在
上是“相邻函数”,否则称它们在![]() 上是“非相邻函数”.例如,点
上是“非相邻函数”.例如,点![]() 与
与![]() 分别是两个函数
分别是两个函数![]() 与
与![]() 图象上的任一点,当
图象上的任一点,当![]() 时,
时, ![]() ,通过构造函数
,通过构造函数![]() 并研究它在
并研究它在![]() 上的性质,得到该函数值得范围是
上的性质,得到该函数值得范围是![]() ,所以
,所以![]() 成立,因此这两个函数在
成立,因此这两个函数在![]() 上是“相邻函数”.
上是“相邻函数”.
(![]() )判断函数
)判断函数![]() 与
与![]() 在
在![]() 上是否为“相邻函数”,并说明理由.
上是否为“相邻函数”,并说明理由.
(![]() )若函数
)若函数![]() 与
与![]() 在
在![]() 上是“相邻函数”,求
上是“相邻函数”,求![]() 的取值范围.
的取值范围.
(![]() )若函数
)若函数![]() 与
与![]() 在
在![]() 上是“相邻函数”,直接写出
上是“相邻函数”,直接写出![]() 的最大值与最小值.
的最大值与最小值.
【答案】(1)见解析(2)![]() ;(3)
;(3)![]() 的最大值为
的最大值为![]() ,
, ![]() 的最小值为
的最小值为![]() .
.
【解析】(1)直接利用相邻函数的定义结合一次函数增减性,得出当x=0时,函数有最大值1,当x=-2时,函数有最小值-1,即-1≤y≤1,进而判断即可;
(2)直接利用相邻函数的定义结合二次函数增减性,得出当x=1时,函数有最大值a-1,当x=0,或x=2时,函数有最大值a,即a-1≤y≤a,进而判断即可;
(3)直接利用相邻函数的定义结合函数增减性,得出当x=1时,函数有最大值a-2,当x=2时,函数有最大值![]() ,即a-2≤y≤
,即a-2≤y≤![]() ,进而判断即可.
,进而判断即可.
解:(![]() )函数
)函数![]() 与
与![]() ,在
,在![]() 上为“相邻函数”.
上为“相邻函数”.
∵![]() ,
,
∴为相邻函数.
(![]() )
)![]()
![]()
![]() .
.
∴![]() .
.
①当![]() ,即
,即![]() 时.
时.
![]() ,
,
∴![]() 无解.
无解.
②![]() ,即
,即![]() 时,
时,
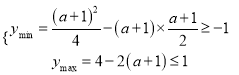
∴![]() .
.
③![]() 即
即![]() 时.
时.
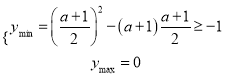 .
.
∴![]() 无解.
无解.
④当![]() 即
即![]() 时.
时.
![]() ,
,
∴![]() ,无解.
,无解.
综上所得: ![]() .
.
(![]() )∵当
)∵当![]() 时
时![]() .
.
![]() 时,
时, ![]() .
.
∴![]() ,
,
∴![]() .
.
当![]() 时
时![]() ,
,
![]() 时
时![]() .
.
∴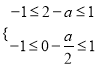 ,
,
∴![]() .
.
综上所得: ![]() 与
与![]() 在
在![]() 上,
上,
是“相邻函数”时.
![]() 的最大值为
的最大值为![]() .
.
![]() 的最小值为
的最小值为![]() .
.
“点睛”此题主要考查了函数的综合以及函数增减性和新定义,根据题意正确理解“相邻函数”的定义是解题关键.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4 层的任意一层出电梯,并设甲在a层出电梯,乙在b层出电梯.
(1)请你用画树状图或列表法求出甲、乙二人在同一层楼出电梯的概率;
(2)小亮和小芳打赌说:“若甲、乙在同一层或相邻楼层出电梯,则小亮胜,否则小芳胜”.该游戏是否公平?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的是_________(只填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2。有下列结论:①4a+b=0;②16a+4b+c<0;③8a+7b+2c>0;④当x>-1时,y的值随x的增大而增大。其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂准备购买![]() 、
、![]() 、
、![]() 三种配件共
三种配件共![]() 件,要求购买时
件,要求购买时![]() 配件的件数是
配件的件数是![]() 配件数的
配件数的![]() 倍,
倍, ![]() 配件不超过
配件不超过![]() 件,且每种配件都必须买,三种配件的价格如下:
件,且每种配件都必须买,三种配件的价格如下: ![]() 、
、![]() 、
、![]() 三种配件的单价分别为
三种配件的单价分别为![]() 元、
元、![]() 元、
元、![]() 元.
元.
(![]() )求购买
)求购买![]() 配件的件数范围.
配件的件数范围.
(![]() )三种配件应各买多少件,才能使买配件的总费用最少?总费用最少多少元?
)三种配件应各买多少件,才能使买配件的总费用最少?总费用最少多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)尺规作图:如图1,在四边形ABCD内找一点P,使得点P到AB、BC的距离相等,并且点P到点A、D的距离也相等.(不写作法,保留作图痕迹).
(2)如图2,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上,①△ABC的面积为______.
②在图中画出与△ABC关于直线l成轴对称的△A1B1C1.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com