
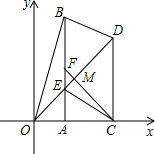
 化时,Rt△OAB的面积恒为
化时,Rt△OAB的面积恒为| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| t |
| 2 |
| 1 |
| t |
| 2 |
| 1 |
| t2 |
| 2 |
| 1 |
| t |
| 1 |
| t |
| 2 |
| 1 |
| t |
| 1 |
| t |
| 2 |
| 1 |
| t |
| 2 |
| 1 |
| t |
| 2 |
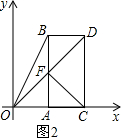
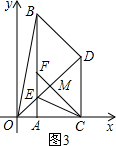
 (3)解法一:若OB=BD,则OB2=BD2.
(3)解法一:若OB=BD,则OB2=BD2.| 1 |
| t2 |
| 1 |
| t2 |
| 1 |
| t2 |
| 2 |
| 1 |
| t |
| 1 |
| t |
| 2 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| 2 |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| t2 |
| 1 |
| t2 |
| 2 |
| 1 |
| t |
| 1 |
| t |
| 2 |
| 2 |
| 2 |
| 1 |
| t |
| 2 |
| 2 |
| 1 |
| t |
| 2 |
| 2 |
| 2 |
| 1 |
| t |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| t |
| 1 |
| t |
| 2 |
 
练习册系列答案
相关习题
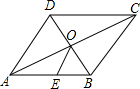
科目:初中数学 来源:不详 题型:解答题 如图:四边形ABCD是菱形,对角线AC与BD相交于O,菱形ABCD的周长是20,BD=6. (1)求AC的长. (2)求菱形ABCD的高DE的长.  查看答案和解析>> 科目:初中数学 来源:不详 题型:单选题 如图,下列条件之一能使平行四边形ABCD是菱形的为( ) ①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
 查看答案和解析>> 科目:初中数学 来源:不详 题型:单选题 如图,在菱形ABCD中,对角线AC、BD相交于点O.点E为边AB的中点,且BD=6, AC=8,则OE长为( )
 查看答案和解析>> 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |