
【题目】如图,四边形ABCD中,AB=CB,AD=CD,对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E、F.求证:OE=OF.

科目:初中数学 来源: 题型:
【题目】(1)拼一拼,画一画:请你用4个长为a,宽为b的矩形拼成一个大正方形,并且正中间留下一个洞,这个洞恰好是一个小正方形。

(2)用不同方法计算中间的小正方形的面积,聪明的你能发现什么?
(3)当拼成的这个大正方形边长比中间小正方形边长多3cm时,它的面积就多24cm2,求中间小正方形的边长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是半圆,连接AB,点O为AB的中点,点C,D在
是半圆,连接AB,点O为AB的中点,点C,D在 ![]() 上,连接AD,CO,BC,BD,OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
上,连接AD,CO,BC,BD,OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( ) 
A.26°
B.28°
C.30°
D.32°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形![]() 中,
中,![]() 是
是![]() 上一动点,点
上一动点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() .
.
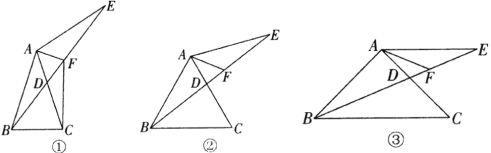
(1)如图①,连接![]() ,求证:
,求证: ![]() ;
;
(2)如图②,当![]() 时,求证:
时,求证: ![]() ;
;
(3)如图③,当![]() 时,若
时,若![]() 平分
平分![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个三角形的两条边长分别是1cm和2cm,一个内角为40度.
(1)请你借助图1画出一个满足题设条件的三角形;
(2)你是否还能画出既满足题设条件,又与(1)中所画的三角形不全等的三角形?若能,请你在图1的右边用“尺规作图”作出所有这样的三角形;若不能,请说明理由;
(3)如果将题设条件改为“三角形的两条边长分别是3cm和4cm,一个内角为40°”,那么满足这一条件,且彼此不全等的三角形共有几个.
友情提醒:请在你画的图中标出已知角的度数和已知边的长度,“尺规作图”不要求写作法,但要保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D与点E恰好重合于点O,则∠A′OB′的度数是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意解答
(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得线段BE、EF、FD之间的数量关系为 .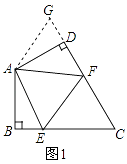
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF= ![]() ∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
(3)如图3,点A在点O的北偏西30°处,点B在点O的南偏东70°处,且AO=BO,点A沿正东方向移动249米到达E处,点B沿北偏东50°方向移动334米到达点F处,从点O观测到E、F之间的夹角为70°,根据(2)的结论求E、F之间的距离.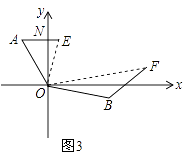
查看答案和解析>>
科目:初中数学 来源: 题型:
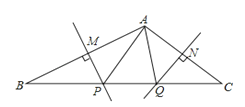
【题目】如图,在△ABC中,AB的垂直平分线分别交AB、BC于点M、P,AC的垂直平分线分别交AC、BC于点N、Q,∠BAC=110°,则∠PAQ=_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=60°,∠B=58°.甲、乙两人想在△ABC外部取一点D,使得△ABC与△DCB全等,其作法如下:
(甲)①作∠A的角平分线L.
②以B为圆心,BC长为半径画弧,交L于D点,则D即为所求.
(乙)①过B作平行AC的直线L.
②过C作平行AB的直线M,交L于D点,则D即为所求.
对于甲、乙两人的作法,下列判断何者正确?( )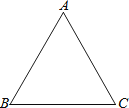
A.两人皆正确
B.两人皆错误
C.甲正确,乙错误
D.甲错误,乙正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com