
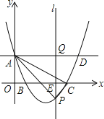
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与
,与![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() ,且
,且![]() ,直线
,直线![]() 轴,在
轴,在![]() 轴上有一动点
轴上有一动点![]() 过点
过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() 与抛物线、直线
与抛物线、直线![]() 的交点分别为
的交点分别为![]() 、
、![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 当
当![]() 时,求
时,求![]() 面积的最大值;
面积的最大值;
![]() 当
当![]() 时,是否存在点
时,是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出此时
相似?若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() (2)12 (3)
(2)12 (3)![]() 或
或![]() 或
或![]()
【解析】
(1)认真审题,直接根据题意列出方程组,求出B,C两点的坐标,进而可求出抛物线的解析式;
(2)分0<t<6时和6<t≤8时两种情况进行讨论,据此即可求出三角形的最大值;
(3)以点D为分界点,分2<t≤8时和t>8时两种情况进行讨论,再根据三角形相似的条件,即可得解.
![]() 由题意知
由题意知![]() 、
、![]() 是方程
是方程![]() 的两根,
的两根,
∴![]() ,
,
由
解得: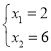
∴![]() 、
、![]()
则![]() ,
,
解得:![]() ,
,
∴该抛物线解析式为:![]() ;
;
![]() 可求得
可求得![]()
设直线![]() 的解析式为:
的解析式为:![]() ,
,
∵![]()
∴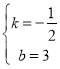
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
要构成![]() ,显然
,显然![]() ,分两种情况讨论:
,分两种情况讨论:
①当![]() 时,设直线
时,设直线![]() 与
与![]() 交点为
交点为![]() ,则:
,则:![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
此时最大值为:![]() ,
,
②当![]() 时,设直线
时,设直线![]() 与
与![]() 交点为
交点为![]() ,则:
,则:![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
当![]() 时,取最大值,最大值为:
时,取最大值,最大值为:![]() ,
,
综上可知,当![]() 时,
时,![]() 面积的最大值为
面积的最大值为![]() ;
;
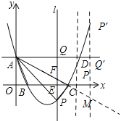
![]() 如图,连接
如图,连接![]() ,则
,则![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,
,![]() ,
,
若:![]() ,则:
,则:![]() ,
,
即: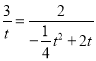 ,
,
∴![]() (舍),或
(舍),或![]() ,
,
若![]() ,则:
,则:![]() ,
,
即: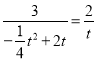 ,
,
∴![]() (舍)或
(舍)或![]() (舍),
(舍),
②当![]() 时,
时,![]() ,
,![]() ,
,
若:![]() ,则:
,则:![]() ,
,
即: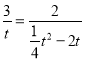 ,
,
∴![]() (舍),或
(舍),或![]() ,
,
若![]() ,则:
,则:![]() ,
,
即: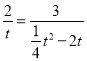 ,
,
∴![]() (舍)或
(舍)或![]() ,
,
∴![]() 或
或![]() 或
或![]() .
.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】正方形![]() 的边长为4,点
的边长为4,点![]() 在对角线
在对角线![]() 上(可与点
上(可与点![]() 重合),
重合),![]() ,点
,点![]() 在正方形的边上.下面四个结论中,
在正方形的边上.下面四个结论中,
①存在无数个四边形![]() 是平行四边形;
是平行四边形;
②存在无数个四边形![]() 是菱形;
是菱形;
③存在无数个四边形![]() 是矩形;
是矩形;
④至少存在一个四边形![]() 是正方形.
是正方形.
所有正确结论的序号是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图①是一个三角形,分别连接三边中点得图②,再分别连接图②中的小三角形三边中点,得图③……按此方法继续下去.

在第![]() 个图形中有______个三角形(用含
个图形中有______个三角形(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安市的大雁塔又名“慈恩寺塔”,是国家级文物保护单位,玄奘为保存由天竺经丝绸之路带回长安的经卷主持修建了大雁塔,最初五层,后加盖至九层,是西安市的标志性建筑之一,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点G处,这时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米,请你根据以上数据,计算大雁塔的高度AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民开始选购家用净水器.一商家抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元?(注:毛利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家教育部提出“每天锻炼一小时,健康工作五十年,幸福生活一辈子”.万州区某中学对九年级部分学生进行问卷调查“你最喜欢的锻炼项目是什么?”,规定从“打球”,“跑步”,“游泳”,“跳绳”,“其他”五个选项中选择自己最喜欢的项目,且只能选择一个项目,并将调查结果绘制成如下两幅不完整的统计图.
最喜欢的锻炼项目 | 人数 |
打球 | 120 |
跑步 |
|
游泳 |
|
跳绳 | 30 |
其他 |
|
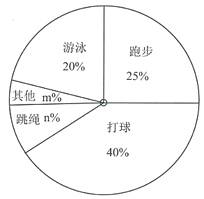
(1)这次问卷调查的学生总人数为 ,人数![]() ;
;
(2)扇形统计图中,![]() ,“其他”对应的扇形的圆心角的度数为 度;
,“其他”对应的扇形的圆心角的度数为 度;
(3)若该年级有1200名学生,估计喜欢“跳绳”项目的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
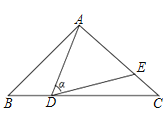
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cos∠α=![]() ,下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或
,下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或![]() ;④0<CE≤6.4.其中正确的结论是_________.(把你认为正确结论的序号都填上)
;④0<CE≤6.4.其中正确的结论是_________.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是半圆的直径,
是半圆的直径,![]() 为半圆
为半圆![]() 的圆心,
的圆心,![]() 是弦,取
是弦,取![]() 的中点
的中点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
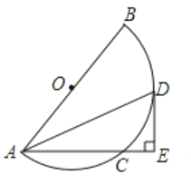
(1)求证:![]() 是半圆
是半圆![]() 的切线;
的切线;
(2)当![]() ,
,![]() 时,求
时,求![]() 的长;
的长;
(3)当![]() 时,直接写出
时,直接写出![]() 面积最大时,点
面积最大时,点![]() 到直径
到直径![]() 的距离.
的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个体地摊经销一批小商品,每件商品的成本为8元.据市场分析,销售单价定为10元时,每天能售出200件;现采用提高商品售价,减少销售量的办法增加利润,若销售单价每涨1元,每天的销售量就减少20件,设销售单价为每件x元,销售量为y件.
(1)写出y与x函数关系式.
(2)若想每天的销售利润恰为640元,同时又要使顾客得到实惠,这种小商品每件售价应定为多少元?
(3)这种小商品每件售价应定为多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com