
 如图,直线l经过点A(4,0),B(0,3).
如图,直线l经过点A(4,0),B(0,3).分析 (1)把点A(4,0),B(0,3)代入直线l的解析式y=kx+b,即可求出结果.
(2)先画出示意图,在Rt△ABM中求出sin∠BAM,然后在Rt△AMC中,利用锐角三角函数的定义求出AM,继而可得点M的坐标.
解答 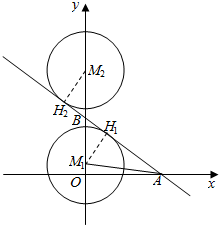 解:
解:
方法一:
(1)∵A(4,0),B(0,3),
∴直线l的解析式为:y=-$\frac{3}{4}$x+3;
(2)作MH⊥AB,垂足为H,
∵M在y轴上,∴设M(0,t),
2S△ABM=BM×AO=AB×MH,
∴|3-t|×4=5×2,
∴t1=$\frac{1}{2}$,t2=$\frac{11}{2}$,
∴M1(0,$\frac{1}{2}$),M2(0,$\frac{11}{2}$).
方法二:
(1)∵直线l经过点A(4,0),B(0,3),
∴设直线l的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{0=4k+b}\\{3=b}\end{array}\right.$
∴$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=3}\end{array}\right.$.
∴直线l的解析式为:y=-$\frac{3}{4}$x+3;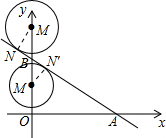
(2)设M坐标为(0,m)(m>0),即OM=m,
若M在B点下边时,BM=3-m,
∵∠MBN′=∠ABO,∠MN′B=∠BOA=90°,
∴△MBN′∽△ABO,
∴$\frac{MN′}{OA}$=$\frac{BM}{AB}$,即 $\frac{2}{4}$=$\frac{3-m}{5}$,
解得:m=$\frac{1}{2}$,此时M(0,$\frac{1}{2}$);
若M在B点上边时,BM=m-3,
同理△BMN∽△BAO,则有 $\frac{MN}{OA}$=$\frac{BM}{AB}$,即 $\frac{2}{4}$=$\frac{m-3}{5}$,
解得:m=$\frac{11}{2}$.此时M(0,$\frac{11}{2}$).
点评 本题考查了用待定系数法求函数的解析式,切线的性质,解答本题的关键是画出示意图,熟练掌握切线的性质及锐角三角函数的定义,难度一般.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
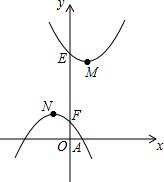 如图,已知二次函数L1:y=ax2-2ax+a+3(a>0)和二次函数L2:y=-a(x+1)2+1(a>0)图象的顶点分别为M,N,与y轴分别交于点E,F.
如图,已知二次函数L1:y=ax2-2ax+a+3(a>0)和二次函数L2:y=-a(x+1)2+1(a>0)图象的顶点分别为M,N,与y轴分别交于点E,F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲、乙均可 | B. | 甲 | C. | 乙 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的弦,AC是⊙O切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )
如图,AB是⊙O的弦,AC是⊙O切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )| A. | 20° | B. | 25° | C. | 40° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
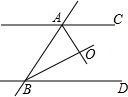 如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么∠BAO与∠ABO之间的大小关系一定为( )
如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么∠BAO与∠ABO之间的大小关系一定为( )| A. | 互余 | B. | 相等 | C. | 互补 | D. | 不等 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
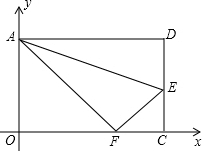 如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为(10,3).
如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为(10,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com