
【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.
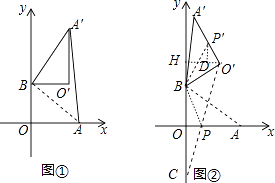
(1)如图①,若α=90°,求AA′的长;
(2)如图②,若α=120°,求点O′的坐标;
(3)在(Ⅱ)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可)
【答案】
(1)
解:如图①,
∵点A(4,0),点B(0,3),
∴OA=4,OB=3,
∴AB= ![]() =5,
=5,
∵△ABO绕点B逆时针旋转90°,得△A′BO′,
∴BA=BA′,∠ABA′=90°,
∴△ABA′为等腰直角三角形,
∴AA′= ![]() BA=5
BA=5 ![]()
(2)
解:作O′H⊥y轴于H,如图②,
∵△ABO绕点B逆时针旋转120°,得△A′BO′,
∴BO=BO′=3,∠OBO′=120°,
∴∠HBO′=60°,
在Rt△BHO′中,∵∠BO′H=90°﹣∠HBO′=30°,
∴BH= ![]() BO′=
BO′= ![]() ,O′H=
,O′H= ![]() BH=
BH= ![]() ,
,
∴OH=OB+BH=3+ ![]() =
= ![]() ,
,
∴O′点的坐标为( ![]() ,
, ![]() )
)
(3)
解:∵△ABO绕点B逆时针旋转120°,得△A′BO′,点P的对应点为P′,
∴BP=BP′,
∴O′P+BP′=O′P+BP,
作B点关于x轴的对称点C,连结O′C交x轴于P点,如图②,
则O′P+BP=O′P+PC=O′C,此时O′P+BP的值最小,
∵点C与点B关于x轴对称,
∴C(0,﹣3),
设直线O′C的解析式为y=kx+b,
把O′( ![]() ,
, ![]() ),C(0,﹣3)代入得
),C(0,﹣3)代入得 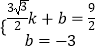 ,解得
,解得 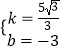 ,
,
∴直线O′C的解析式为y= ![]() x﹣3,
x﹣3,
当y=0时, ![]() x﹣3=0,解得x=
x﹣3=0,解得x= ![]() ,则P(
,则P( ![]() ,0),
,0),
∴OP= ![]() ,
,
∴O′P′=OP= ![]() ,
,
作P′D⊥O′H于D,
∵∠BO′A=∠BOA=90°,∠BO′H=30°,
∴∠DP′O′=30°,
∴O′D= ![]() O′P′=
O′P′= ![]() ,P′D=
,P′D= ![]() O′D=
O′D= ![]() ,
,
∴DH=O′H﹣O′D= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴P′点的坐标为( ![]() ,
, ![]() )
)
【解析】本题考查了几何变换综合题:熟练掌握旋转的性质;理解坐标与图形性质;会利用两点之间线段最短解决最短路径问题;记住含30度的直角三角形三边的关系.(1)如图①,先利用勾股定理计算出AB=5,再根据旋转的性质得BA=BA′,∠ABA′=90°,则可判定△ABA′为等腰直角三角形,然后根据等腰直角三角形的性质求AA′的长;(2)作O′H⊥y轴于H,如图②,利用旋转的性质得BO=BO′=3,∠OBO′=120°,则∠HBO′=60°,再在Rt△BHO′中利用含30度的直角三角形三边的关系可计算出BH和O′H的长,然后利用坐标的表示方法写出O′点的坐标;(3)由旋转的性质得BP=BP′,则O′P+BP′=O′P+BP,作B点关于x轴的对称点C,连结O′C交x轴于P点,如图②,易得O′P+BP=O′C,利用两点之间线段最短可判断此时O′P+BP的值最小,接着利用待定系数法求出直线O′C的解析式为y= ![]() x﹣3,从而得到P(
x﹣3,从而得到P( ![]() ,0),则O′P′=OP=
,0),则O′P′=OP= ![]() ,作P′D⊥O′H于D,然后确定∠DP′O′=30°后利用含30度的直角三角形三边的关系可计算出P′D和DO′的长,从而可得到P′点的坐标.
,作P′D⊥O′H于D,然后确定∠DP′O′=30°后利用含30度的直角三角形三边的关系可计算出P′D和DO′的长,从而可得到P′点的坐标.
【考点精析】本题主要考查了线段的基本性质和含30度角的直角三角形的相关知识点,需要掌握线段公理:所有连接两点的线中,线段最短.也可简单说成:两点之间线段最短;连接两点的线段的长度,叫做这两点的距离;线段的大小关系和它们的长度的大小关系是一致的;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半才能正确解答此题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】为了解某校学生的身高情况,随机抽取该校若干男生、女生进行抽样调查.已知抽取的样本中,男生、女生人数相同,利用所得数据绘制如下统计表和统计图(如图20-3-2所示):
身高情况分组表(单位:cm)
组别 | 身高 |
A | x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | x≥170 |
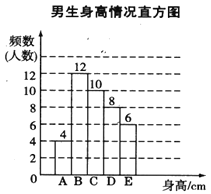
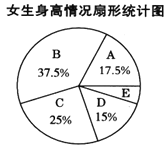
根据图表提供的信息,回答下列问题:
(1)样本中,男生身高的众数在___________组,中位数在___________组;
(2)样本中,女生身高在E组的有___________人;
(3)已知该校共有男生400人、女生380人,请估计身高在160≤x<170范围内的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.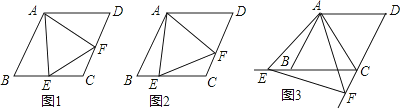
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,△ABC中,∠ABC、∠ACB的平分线交于O点,过O点作EF∥BC交AB、AC于点E、F.试猜想EF、BE、CF之间有怎样的关系,并说明理由.


(2)如图,若将图①中∠ACB的平分线改为外角∠ACD的平分线,其它条件不变,则刚才的结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)求证:BE=CF;
(2)如果AB=8,AC=6,求AE、BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为 ![]() .
.
其中正确结论的个数是( )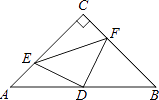
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR,②QP∥AR,③△BPR≌△QPS中一定正确的是( )
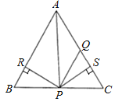
A. 全部正确 B. 仅①和②正确 C. 仅①正确 D. 仅①和③正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场经营的某品牌童装,4月的销售额为20000元,为扩大销量,5月份商场对这种童装打9折销售,结果销量增加了50件,销售额增加了7000元.
(1)求该童装4月份的销售单价;
(2)若4月份销售这种童装获利8000元,6月全月商场进行“六一儿童节”促销活动.童装在4月售价的基础上一律打8折销售,若该童装的成本不变,则销量至少为多少件,才能保证6月的利润比4月的利润至少增长25%?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com