
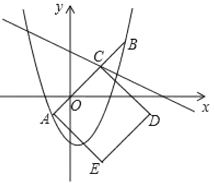
����Ŀ������һ��������������������ͼ���ϴ���һ���㣬���ĺᡢ��������ȣ���ô���������ú����IJ���㣮
��1��һ�κ���![]() �IJ���������Ϊ______��
�IJ���������Ϊ______��
��2�����κ���![]() �����������ֱ�Ϊ��
�����������ֱ�Ϊ��![]() ��
��![]() ��
��![]() ����ࣩ������
����ࣩ������![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת90���õ���
˳ʱ����ת90���õ���![]() �����
�����![]() �����꣮
�����꣮
��3����֪���κ���![]() ����������������Ϊ
����������������Ϊ![]() ��
��
����![]() ��ֵ��
��ֵ��
����ͼ����������![]() ���߶�
���߶�![]() Χ�ɵķ��ͼ�μ���
Χ�ɵķ��ͼ�μ���![]() ����
����![]() Ϊһ�κ���
Ϊһ�κ���![]() �IJ���㣬���߶�
�IJ���㣬���߶�![]() Ϊ��������������
��������������![]() ����
����![]() ������ֻ��һ�����ڷ��ͼ��
������ֻ��һ�����ڷ��ͼ��![]() ���ڲ����������߽磩ʱ�����
���ڲ����������߽磩ʱ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1����1��1������2��![]() ��
��![]() ����3����
����3����![]() ����
����![]() ��
��![]()
��������
��1������һ�κ���y��3x��2��y��x��ɷ����飬��֮���ɵó����ۣ�
��2���������κ���y��x2��3x+1��y��x��ɷ����飬��֮���ɵó���P��Q�����꣬�ɵ�P��Q��ֱ��y��x�ϣ��ɵó���PQRΪ����ֱ�������Σ�����P��PP���QR������Ϊ��P�䣬���ݵ���ֱ�������ε����ʼ��ɵó���R�����ꣻ
��3�������ݵ�A��B�����꣬���ô���ϵ�����������a��b��ֵ��
������һ�κ���y����![]() x+m��y��x�ɷ����飬��֮���ɵó���C�����꣬���������ε����ʿɵó���D��E�����꣬��ֻ�е�D��ͼ��M���ڲ���ֻ�е�E��ͼ��M���ڲ���������ҳ�����m�IJ���ʽ�飬��֮���ɵó����ۣ�����ֻд�𰸲�д���̵Ŀ���ֱ�Ӵ����D��E�����꣬���ü����ҳ�m��ȡֵ��Χ����
x+m��y��x�ɷ����飬��֮���ɵó���C�����꣬���������ε����ʿɵó���D��E�����꣬��ֻ�е�D��ͼ��M���ڲ���ֻ�е�E��ͼ��M���ڲ���������ҳ�����m�IJ���ʽ�飬��֮���ɵó����ۣ�����ֻд�𰸲�д���̵Ŀ���ֱ�Ӵ����D��E�����꣬���ü����ҳ�m��ȡֵ��Χ����
�⣺��1����������ã�![]() ��
��
��ã�![]() ��
��
��һ�κ���y��3x��2�IJ����������Ϊ��1��1����
��2����������ã�![]() ��
��
��ã�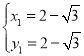 ��
��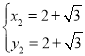 ��
��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�ߵ�P��Q��ֱ��y��x�ϣ�
���QPR��45�㣬
���PQRΪ����ֱ�������Σ�
����P��PP���QR������Ϊ��P�䣬��ͼ1��ʾ��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
��3�����߶��κ���y��ax2+bx��3����������������ΪA����1����1����B��3��3����
![]()
![]() ��
��
��ã�![]() ��
��
��![]()
 ����ã�
����ã�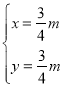 ��
��
![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��
���ı���ACDEΪ�����Σ���A��C��ֱ��y��x�ϣ�A����1����1����
![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��ֻ�е�![]() ��ͼ��
��ͼ��![]() ���ڲ�ʱ����
���ڲ�ʱ���� ��
��
���![]() ��
��
��ֻ�е�![]() ��ͼ��
��ͼ��![]() ���ڲ�ʱ����
���ڲ�ʱ����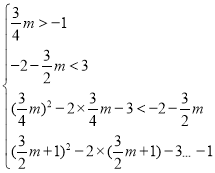 ��
��
��ã�![]() ��
��
����������![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ![]() ��
��![]() ��
��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı���![]() �У��Խ���
�У��Խ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() �Ƶ�
�Ƶ�![]() ����ʱ�뷽����ת�õ�
����ʱ�뷽����ת�õ�![]() ����ת��Ϊ����0��������90����������
����ת��Ϊ����0��������90����������![]() ��
��![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
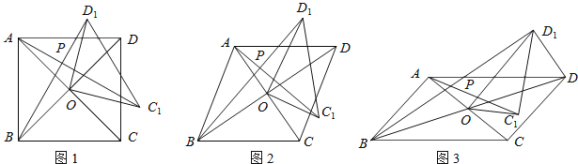
��1����ͼ1�����ı���![]() �������Σ�
��������
����֤��![]() ��
��![]() ��
��
����ֱ��д��![]() ��
��![]() ��λ�ù�ϵ��
��λ�ù�ϵ��
��2����ͼ2�����ı���![]() �����Σ�
������![]() ��
��![]() ����
����![]() ���ж�
���ж�![]() ��
��![]() ��λ�ù�ϵ��˵�����ɣ������
��λ�ù�ϵ��˵�����ɣ������![]() ��ֵ��
��ֵ��
��3����ͼ3�����ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�![]() ��
��![]() ������
������![]() ����
����![]() ����ֱ��д��
����ֱ��д��![]() ��ֵ��
��ֵ��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
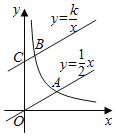
����Ŀ����ͼ��ֱ��y��![]() x��˫����y��
x��˫����y��![]() ��k��0��x��0�����ڵ�A����ֱ��y��
��k��0��x��0�����ڵ�A����ֱ��y��![]() x����ƽ��2����λ���Ⱥ���y�ύ�ڵ�C����˫���߽��ڵ�B����OA��3BC����k��ֵΪ____��
x����ƽ��2����λ���Ⱥ���y�ύ�ڵ�C����˫���߽��ڵ�B����OA��3BC����k��ֵΪ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��3��25����ȫ����Сѧ����ȫ�����գ�ǰ����ѧΪ��ǿѧ���İ�ȫ��ʶ����ȫУѧ���μӰ�ȫ֪ʶ���������г�ȡ�˲���ѧ���ɼ�(�÷�ȡ������������Ϊ100��)�����ȼ�����ͳ��(![]() ����
����![]() ��-
��-![]() �֣�
�֣�![]() ����
����![]() ��
��![]() �֣�
�֣�![]() ����
����![]() ��
��![]() �֣�
�֣�![]() ����
����![]() ��
��![]() �֣�
�֣�![]() ����
����![]() ��
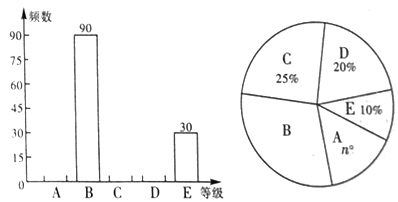
��![]() ��)������ͳ�ƽ�����Ƴ����������в�������ͳ��ͼ��������ͼ��������Ϣ����������⣺
��)������ͳ�ƽ�����Ƴ����������в�������ͳ��ͼ��������ͼ��������Ϣ����������⣺
��1��![]() _______��
_______��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����У����![]() ��ѧ�������ɼ���
��ѧ�������ɼ���![]() ������(��
������(��![]() ��)��ѧ����ȫ��ʶ��ǿ���д���������ǿ��ȫ���������У��ȫ��ʶ��ǿ��ѧ��Լ�ж�����?
��)��ѧ����ȫ��ʶ��ǿ���д���������ǿ��ȫ���������У��ȫ��ʶ��ǿ��ѧ��Լ�ж�����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ҵ�ķ�չ����Ч�ٽ��ҹ��ִ�������.ij�������۹�˾2016��ӯ��1500��Ԫ����2018��ӯ��2160��Ԫ���Ҵ�2016�굽2018�꣬ÿ��ӯ��������������ͬ.
��1����ÿ��ӯ�����������ʣ�
��2�����ù�˾ӯ�����������ʼ������ֲ��䣬��ô2019��ù�˾ӯ���ܷ�ﵽ2500��Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
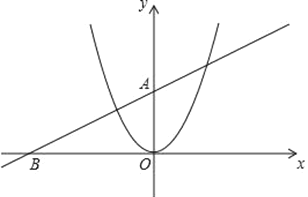
����Ŀ����ֱ֪��y��kx+b������A��0��2����B����4��0����������y��x2��
��1����ֱ�ߵĽ���ʽ��
��2����������y��x2����x������ƽ�ƣ�ƽ�ƺ�������߶Գ�����ಿ����y�ύ�ڵ�C���Գ����Ҳಿ����������ֱ��y��kx+b���ڵ�D������CD����CD��x��ʱ����ƽ�ƺ�õ��������ߵĽ���ʽ��
��3���ڣ�2���������£�ƽ�ƺ�õ��������ߵĶԳ�����x�ύ�ڵ�E��PΪ����������һ���㣬����P�������߶Գ���Ĵ��ߣ�����ΪQ���Ƿ���������ĵ�P��ʹ�Ե�E��P��QΪ���������������AOB���ƣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[�Ķ�����]
����֪��:![]() ����ô
����ô![]() ������ڶ�����?
������ڶ�����?
��ͼ1��ʾ�ĵȱ������������У���![]() �е�һ��С�ȱ��������е���Ϊ
�е�һ��С�ȱ��������е���Ϊ![]() ����
����![]() ��
��![]() �е�����С�ȱ��������е����ĺ���
�е�����С�ȱ��������е����ĺ���![]() ��
��![]() ; ������
; ������![]() �е�
�е�![]() ��С�ȱ��������е����ĺ���
��С�ȱ��������е����ĺ���![]() ������
������![]() ���õȱ������������й���
���õȱ������������й���![]() С�ȱ������Σ�����С�ȱ����������ĺ�Ϊ
С�ȱ������Σ�����С�ȱ����������ĺ�Ϊ![]() ��
��
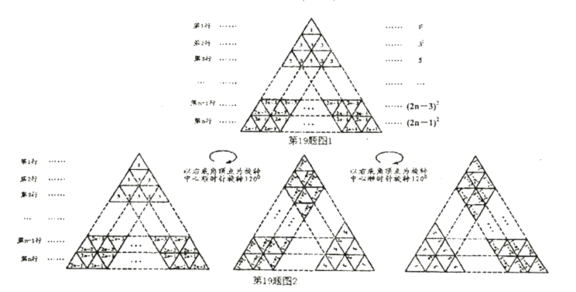
[����̽��]
��ͼ1�еĵȱ�������������ҵǶ���Ϊ��ת����˳ʱ����ת![]() �ٰ���ת���ͼ�ΰ�ͬ���ķ����ɵ���ͼ2��ʾ�����������۲��������ȱ��������������ͬһλ�õ�С�ȱ��������е���������λ������λ�õ�������(���
�ٰ���ת���ͼ�ΰ�ͬ���ķ����ɵ���ͼ2��ʾ�����������۲��������ȱ��������������ͬһλ�õ�С�ȱ��������е���������λ������λ�õ�������(���![]() �еĵ�
�еĵ�![]() ��С�������е����ֱ�Ϊ
��С�������е����ֱ�Ϊ![]() �ĺ�Ϊ
�ĺ�Ϊ![]() ;����λ��ż��λ�õ�������(���
;����λ��ż��λ�õ�������(���![]() �еĵ�
�еĵ�![]() ��С�������е����ֱ�Ϊ
��С�������е����ֱ�Ϊ![]() �ĺ�Ϊ
�ĺ�Ϊ![]() ;��ÿ���ȱ������������У�����λ������λ�õ�����λ��ż��λ�õ�����
;��ÿ���ȱ������������У�����λ������λ�õ�����λ��ż��λ�õ�����![]() ������λ��ż��λ�õ�����_
������λ��ż��λ�õ�����_
��![]()
��ˣ�![]()
[�������]�������Ϸ��֣�����:![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���![]() ������˵����ȷ�ĸ����ǣ�������
������˵����ȷ�ĸ����ǣ�������
�ٶ����κ�����������![]() ���ö��κ�����ͼ������
���ö��κ�����ͼ������![]() ��
��![]() ���㣻
���㣻
�����ú���ͼ��ĶԳ���Ϊֱ��![]() �������
�������![]() ��
��
�۵�![]() ʱ��
ʱ��![]() ��
��![]() �����������
�����������
����![]() ��
��![]() �Ǻ���ͼ���ϵ����㣬���
�Ǻ���ͼ���ϵ����㣬���![]() �ܳ�������
�ܳ�������![]() ��
��
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�Խ�ͨ������˽������ȫУ��������˲���ѧ������������Ϊ���֣�![]() ���dz��˽⣬
���dz��˽⣬![]() ���Ƚ��˽⣬
���Ƚ��˽⣬![]() �������˽⣬
�������˽⣬![]() ����̫�˽⣬�����˴ε������������Ƴ����治����������ͳ��ͼ������ͳ��ͼ��
����̫�˽⣬�����˴ε������������Ƴ����治����������ͳ��ͼ������ͳ��ͼ��
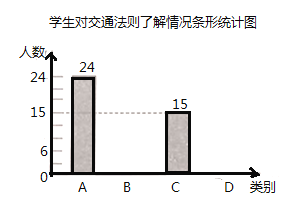
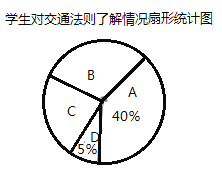
��1�����ι�����_______��ѧ��������ͳ��ͼ��![]() ����Ӧ���ε�Բ�ĽǶ�����_______��
����Ӧ���ε�Բ�ĽǶ�����_______��
��2����ȫ����ͳ��ͼ��
��3��ѧУ���Ӽס��ҡ���������λѧ���������ȡ����ѧ���μ�������ͨ���澺���������б�����״ͼ�ķ������������ѧ��ͬʱ��ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com