
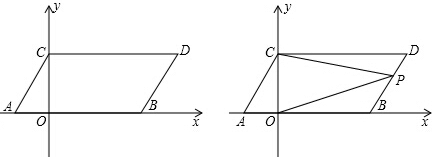
分析 (1)根据非负数的性质得到m=-2,n=5,求得A(-2,0),B(5,0),根据平移的性质得到点C(0,3),D(7,3),即可得到结果;
(2)过点P作PE∥CD,根据两直线平行,内错角相等可得∠DCP=∠CPE,根据平行公理可得PE∥AB,再根据两直线平行,内错角相等可得∠BOP=∠OPE,然后求出∠DCP+∠BOP=∠CPE+∠OPE=∠CPO,再求出∠DCP,∠BOP与∠CPO的数量关系即可;
(3)过P作PM⊥OB于M,并反向延长交CD于N,设P(x,y),根据S△POB:S△POC=5:6,于是得到x=2y;由于S△PCD=S△PBD,于是得到$\frac{1}{2}$×7•(3-y)=18-$\frac{1}{2}$×7(3-y)-$\frac{1}{2}$×3x-$\frac{1}{2}$×5y,最后解方程组即可得到结论.
解答 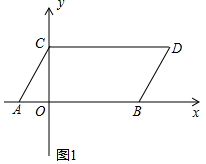 解:(1)|m+2|+$\sqrt{5-n}$=0,
解:(1)|m+2|+$\sqrt{5-n}$=0,
∴m=-2,n=5,
∴A(-2,0),B(5,0),
∵点A,B分别向上平移3个单位,再向右平移2个单位,
∴C(0,3),D(7,2);
∵OB=5,
∴S四边形OBDC=$\frac{1}{2}$(5+7)×3=18;
(2)∠DCP+∠BOP=∠CPO.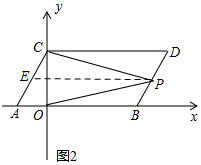
理由:由平移的性质可得AB∥CD,
如图2,过点P作PE∥AB,则PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP,
∴∠DCP,∠BOP与∠CPO的数量关系为:∠DCP+∠BOP=∠CPO;
(3)存在,
如图3,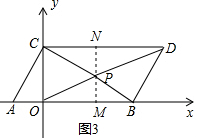 过P作PM⊥OB于M,交CD于N,
过P作PM⊥OB于M,交CD于N,
∵CD∥OB,
∴PN⊥CD,
设P(x,y),
∵S△POB:S△POC=5:6,
∴5×$\frac{1}{2}$×3x=6×$\frac{1}{2}$×5y,
∴x=2y,①
∵S△PCD=S△PBD,
∴$\frac{1}{2}$×7•(3-y)=18-$\frac{1}{2}$×7(3-y)-$\frac{1}{2}$×3x-$\frac{1}{2}$×5y,②
由①、②解得x=4,y=2,
∴P(4,2),即P在四边形OBDC内,
故在四边形OBDC内存在点P(4,2),使S△PCD=S△PBD;S△POB:S△POC=5:6.
点评 本题属于三角形综合题,主要考查了坐标与图形性质,平行线的性质,三角形的面积,坐标与图形变化-平移,作辅助线构造平行线和垂线是解题的关键.


科目:初中数学 来源: 题型:选择题
 连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2016次操作后右下角的小正方形面积是( )
连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2016次操作后右下角的小正方形面积是( )| A. | $\frac{1}{2004}$ | B. | ${(\frac{1}{2})^{2016}}$ | C. | ${(\frac{1}{4})^{2016}}$ | D. | $1-{(\frac{1}{4})^{2016}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD与ECGF是两个边长分别为a,b的正方形,写出a,b表示阴影部分面积的代数式,并计算当a=2,b=8时,阴影部分的面积.
如图,四边形ABCD与ECGF是两个边长分别为a,b的正方形,写出a,b表示阴影部分面积的代数式,并计算当a=2,b=8时,阴影部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线AC、DF被三条平行线l1,l2,l3所截,交点分别为A,D,B,E,C,F,且AB=3,BC=5,EF=4,则DE=$\frac{12}{5}$.
如图,直线AC、DF被三条平行线l1,l2,l3所截,交点分别为A,D,B,E,C,F,且AB=3,BC=5,EF=4,则DE=$\frac{12}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
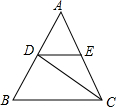 如图,△ABC中,AB=AC=BC,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长是( )
如图,△ABC中,AB=AC=BC,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长是( )| A. | 2a | B. | $\frac{4}{3}$a | C. | $\frac{3}{2}$a | D. | a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com