
【题目】如图,在![]() 中,
中,![]() (圆心
(圆心![]() 在
在![]() 内部)经过
内部)经过![]() 两点,交线段
两点,交线段![]() 于点
于点![]() 直径
直径![]() 交
交![]() 于点
于点![]() 点
点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 落在
落在![]() 上.连结
上.连结![]() .
.
![]() 求证:
求证:![]() .
.
![]() 在圆心
在圆心![]() 的运动过程中,
的运动过程中,
![]() 若
若![]() ,求
,求![]() 的长.
的长.
![]() 若点
若点![]() 关于
关于![]() 的对称点落在
的对称点落在![]() 边上时,求
边上时,求![]() 的值.(直接写出答案)
的值.(直接写出答案)
![]() 令
令![]() 与边
与边![]() 的另一个交点为
的另一个交点为![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() 若
若![]() ,垂足为点
,垂足为点![]() 求证:
求证:![]() .
.
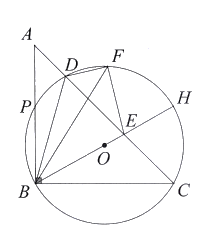
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() 或
或![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)由对称的性质可得∠A=∠BFD,结合∠BFD=∠C,即可推出结论;
(2)①先证∠DFE为直角,设![]() ,再用含a的代数式分别将FE,DE,EC表示出来,根据
,再用含a的代数式分别将FE,DE,EC表示出来,根据![]() 列方程即可求出CE的长;
列方程即可求出CE的长;
②分两种情况讨论,当点F关于AC的对称点落在BF边上时,连接DO,设FF'交AC于点M,证明BD=BE,△BOD是等腰直角三角形,即可求出结果;当点F关于AC的对称点落在BE边上时,点F'与点O重合,证明△DOF为等边三角形,在Rt△DOE中,利用锐角三角函数即可求出结果;
(3)如图作辅助线,先证明△QBG≌△ECM,推出BQ=CE,再证明DQ=DP=AD即可.
解:(1)![]() 点
点![]() 关于直线
关于直线![]() 对称,
对称,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)①![]() 点
点![]() 关于直线
关于直线![]() 对称,
对称,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是直径,
是直径,
![]() 由圆的轴对称性可知:
由圆的轴对称性可知:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 设
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() ;
;
②如图1,当点F关于AC的对称点落在BF边上时,连接DO,设FF'交AC于点M,则AC垂直平分FF',
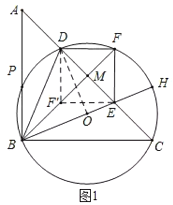
由(1)知,∠A=∠C=45°,∠ABC=90°,
∴BA=BC,∠ABM=∠CBM=45°,
∵点A,F关于直线BD对称,
∴AD=DF,AB=FB,
又∵DB=DB,
∴△ABD≌△FBD(SSS),
∴∠ABD=∠FBD,
∵△BFE≌△BCE,
∴∠FBE=∠CBE,
∴∠ABD=∠FBD=∠FBE=∠CBE=22.5°,
∴∠DBE=∠DBF+∠EBF=45°,
∵OD=OB,
∴∠OBD=∠ODB=45°,
∴∠DOB=90°,
在△BDM与△BEM中,∠BDM=∠BEM=90°22.5°=67.5°,
∴BD=BE,
在等腰Rt△BOD中,设OB=OD=r,则BD=![]() ,
,
∴BE=![]() ,OE=
,OE=![]() ,
,
∴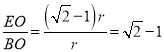 ;
;
如图2,当点F关于AC的对称点落在BE边上时,
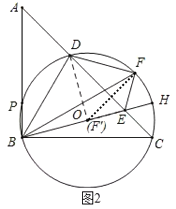
∵∠DF'E=∠DFE=90°,∠DOB=90°
∴点F'与点O重合,
连接OF,则OD=OF=DF,
∴△DOF为等边三角形,
∴∠ODF=60°,
∴∠ODE=∠FDE=30°,
在Rt△DOE中,tan∠ODE=![]() =tan30°=
=tan30°=![]() ,
,
∴![]() ,
,
综上所述,![]() 的值为
的值为![]() 或
或![]() ;
;
(3)连结![]() ;FC交
;FC交![]() 于点
于点![]() ,
,
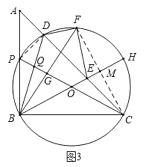
![]() ,
,
∴PC是直径,
∵![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
∵![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级600名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:![]() )分成五组(
)分成五组(![]() :
:![]() ;
;![]() :
:![]() ;
;![]() :
:![]() ;
;![]() :
:![]() ;
;![]() :
:![]() ),并依据统计数据绘制了如下两幅尚不完整的统计图.
),并依据统计数据绘制了如下两幅尚不完整的统计图.
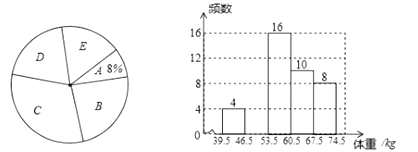
解答下列问题:
(1)这次抽样调查的样本容量是________,并补全频数分布直方图;
(2)![]() 组学生的频率为_________,在扇形统计图中
组学生的频率为_________,在扇形统计图中![]() 组的圆心角是__________度;
组的圆心角是__________度;
(3)请你估计该校初三年级体重超过![]() 的学生大约有多少名?
的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点A的坐标为(0,1),点B的坐标为(1,2),∠ABC=90°,连接AC.
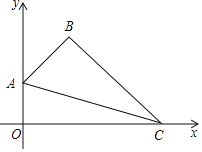
(1)求直线AC的函数表达式;
(2)点P是线段OC上一动点,从点O向点C运动,过点P作PM∥y轴,分别交AB或BC,AC于点M,N,其中点P的横坐标为m,MN的长为n.
①当0<m≤1时,求n与m之间的函数关系式;
②当△AMN的面积最大时,请直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在家乡的楼顶上![]() 处测得池塘的一端
处测得池塘的一端![]() 处的俯角为
处的俯角为![]() ,测得池塘
,测得池塘![]() 处的俯角
处的俯角![]() ,
,![]() 、
、![]() 、
、![]() 三点在同一水平直线上.已知楼高
三点在同一水平直线上.已知楼高![]() 米,求池塘宽
米,求池塘宽![]() 为多少米?(参考数据:
为多少米?(参考数据:![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() .结果保留一位小数.)
.结果保留一位小数.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() )的图象交于
)的图象交于![]() ,
,![]() 两点.
两点.
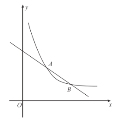
(1)求![]() 的值;
的值;
(2)求出一次函数与反比例函数的表达式;
(3)过点![]() 作
作![]() 轴的垂线,与直线
轴的垂线,与直线![]() 和函数
和函数![]() (
(![]() )的图象的交点分别为点
)的图象的交点分别为点![]() ,
,![]() ,当点
,当点![]() 在点
在点![]() 下方时,写出
下方时,写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() ).
).
(1)求出二次函数图象的对称轴;
(2)若该二次函数的图象经过点![]() ,且整数
,且整数![]() ,
,![]() 满足
满足![]() ,求二次函数的表达式;
,求二次函数的表达式;
(3)对于该二次函数图象上的两点![]() ,
,![]() ,设
,设![]() ,当
,当![]() 时,均有
时,均有![]() ,请结合图象,直接写出
,请结合图象,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
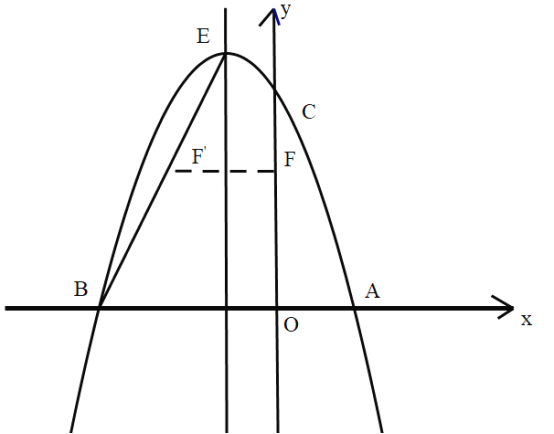
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,直线l是抛物线的对称轴,
,直线l是抛物线的对称轴,![]() 是抛物线的顶点.
是抛物线的顶点.
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)如图,连接![]() ,线段
,线段![]() 上的点
上的点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好在线段
恰好在线段![]() 上,求点
上,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
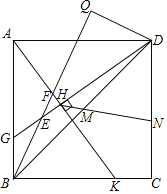
【题目】如图,Q为正方形ABCD外一点,连接BQ,过点D作DQ⊥BQ,垂足为Q,G、K分别为AB、BC上的点,连接AK、DG,分别交BQ于F、E,AK⊥DG,垂足为点H,AF=5,DH=8,F为BQ中点,M为对角线BD的中点,连接HM并延长交正方形于点N,则HN的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com