
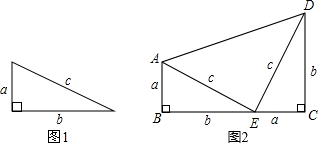
 【定理表述】
【定理表述】分析 【尝试证明】利用S梯形ABCD=SRt△ABE+SRt△DEC+SRt△AED进行证明即可;
【知识拓展】在直角梯形ABCD中,BC<AD,由于已证△AED是直角三角形,那么利用勾股定理有AD=$\sqrt{2}$c,从而可证$\frac{a+b}{c}$<$\sqrt{2}$.
解答 解:【定理表述】如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2.
【尝试证明】
∵Rt△ABE≌Rt△ECD,
∴∠AEB=∠EDC,
又∵∠EDC+∠DEC=90°,
∴∠AEB+∠DEC=90°,
∴∠AED=90°.
∵S梯形ABCD=SRt△ABE+SRt△DEC+SRt△AED,
∴$\frac{1}{2}$(a+b)(a+b)=$\frac{1}{2}$ab+$\frac{1}{2}$ab+$\frac{1}{2}$c2,
整理,得a2+b2=c2.
【知识拓展】
∵AD=$\sqrt{2}$c,BC<AD,
∴a+b<$\sqrt{2}$c,即$\frac{a+b}{c}$<$\sqrt{2}$,
故答案为:$\sqrt{2}$c,<,a+b<$\sqrt{2}$c
点评 本题考查了勾股定理的证明,本题利用了全等三角形的判定和性质、面积分割法、勾股定理等知识.


科目:初中数学 来源: 题型:填空题
| 尺码(cm) | 23.5 | 24 | 24.5 | 25 | 25.5 |
| 销售量(双) | 1 | 2 | 2 | 5 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=CD,AD∥BC | B. | AB∥CD,AB=CD | C. | AB=CD,AD=BC | D. | AB∥CD,AD∥BC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在我校初一年级学生中随机选取100名女生 | |
| B. | 在我校初二年级学生中随机选取100名男生 | |
| C. | 在我校初三年级学生中随机选取100名学生 | |
| D. | 在我校7000多名初中学生中随机选取100名学生 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点E为正方形ABCD的边BC延长线上一点,BF⊥DE于点F,交CD边于点G.
如图,点E为正方形ABCD的边BC延长线上一点,BF⊥DE于点F,交CD边于点G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
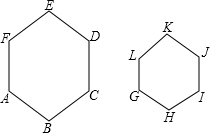 如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论中:
如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论中:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
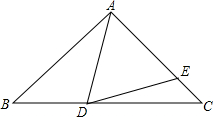 如图,△ABC是等腰三角形,AB=AC,D、E分别是△ABC的边BC、AC上的点,且AD=AE,若∠BAD=46°,则∠EDC=23°.
如图,△ABC是等腰三角形,AB=AC,D、E分别是△ABC的边BC、AC上的点,且AD=AE,若∠BAD=46°,则∠EDC=23°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
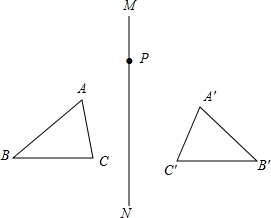
| A. | AP=A′P | B. | MN垂直平分AA′,CC′ | ||
| C. | 这两个三角形的面积相等 | D. | 直线AB、A′B的交点不一定在MN上 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 输入 | … | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 输出 | … | $\frac{1}{2}$ | $\frac{2}{5}$ | $\frac{3}{10}$ | $\frac{4}{17}$ | $\frac{5}{26}$ | $\frac{6}{37}$ | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com