
科目:初中数学 来源: 题型:解答题
 如图,BC为半⊙O的直径,D是弧CA的中点,连接OD,交AC于点F.
如图,BC为半⊙O的直径,D是弧CA的中点,连接OD,交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知⊙O的直径为10,点C是圆内一点,且OC=3.
如图,已知⊙O的直径为10,点C是圆内一点,且OC=3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
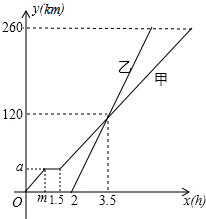 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(甲车休息前后的速度相同),甲、乙两车行驶的路程y(km)与行驶的时间x(h)的函数图象如图所示.根据图象的信息有如下四个说法:
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(甲车休息前后的速度相同),甲、乙两车行驶的路程y(km)与行驶的时间x(h)的函数图象如图所示.根据图象的信息有如下四个说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离:现在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度.
如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离:现在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10的立方根是$\root{3}{10}$ | B. | -2是4的一个平方根 | ||
| C. | $\frac{4}{9}$的平方根是$\frac{2}{3}$ | D. | 0.01的算术平方根是0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com