练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．代数式$\frac{{\sqrt{x}}}{x-2}$有意义时，x应满足的条件为x≥0且x≠2．

    分析 根据被开方数大于等于0，分母不等于0列式计算即可得解．

    解答 解：由题意得，x≥0且x-2≠0，
    解得x≥0且x≠2．
    故答案为：x≥0且x≠2．

    点评 本题考查的知识点为：分式有意义，分母不为0；二次根式的被开方数是非负数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    15．已知⊙O的直径AB=10cm，CD是⊙O的弦，CD⊥AB，垂足为M，且CD=8cm，则AC的长为（　　）
    A．$2\sqrt{5}$B．$2\sqrt{5}$或$4\sqrt{5}$C．$4\sqrt{5}$D．$2\sqrt{5}$或6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．北京时间2015年04月25日14时11分，尼泊尔发生强烈地震，震级8.1级左右．在地震抢救中，某探测队探测出某建筑物下面有生命迹象，为了准确测出生命迹象所在的深度，他们在生命迹象上方建筑物的一侧地面上相距4米的A，B两处，用仪器探测生命迹象C，已知探测线与地面的夹角分别是30°和60°（如图），求该生命迹象所在位置的深度（参考数据：$\sqrt{3}$≈1.732，结果保留一位小数）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知：如图1，抛物线的顶点为M，平行于x轴的直线与该抛物线交于点A，B（点A在点B左侧），根据对称性△AMB恒为等腰三角形，我们规定：当△AMB为直角三角形时，就称△AMB为该抛物线的“完美三角形”．
    （1）①如图2，求出抛物线y=x2的“完美三角形”斜边AB的长；
    ②抛物线y=x2+1与y=x2的“完美三角形”的斜边长的数量关系是相等；
    （2）若抛物线y=ax2+4的“完美三角形”的斜边长为4，求a的值；
    （3）若抛物线y=mx2+2x+n-5的“完美三角形”斜边长为n，且y=mx2+2x+n-5的最大值为-1，求m，n的值．

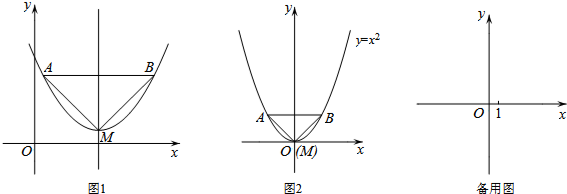
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．计算：$\sqrt{32}-\sqrt{8}$的结果是（　　）
    A．$\sqrt{24}$B．$2\sqrt{6}$C．$3\sqrt{2}$D．$2\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图①，在Rt△ABC和Rt△EDC中，∠ACB=∠ECD=90°，AC=EC=BC=DC，AB与EC交于F，ED与AB、BC分别交于M、H．
    （1）求证：CF=CH；
    （2）如图②，Rt△ABC不动，将Rt△EDC绕点C旋转到∠BCE=45°时，判断四边形ACDM的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．反比例函数y=$\frac{{k}^{2}}{x}$（k为常数，k≠0）的图象位于第一、三象限．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

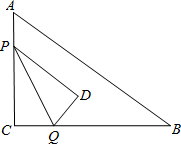    2．在Rt△ABC中，∠C=90°，AC=12，BC=16，动点P从点A出发沿AC边向点C以每秒3个单位长度的速度运动，动点Q从点C出发沿着CB边向点B以每秒4个单位长的速度运动．P、Q分别从点A、C同时出发，当其中一点到达端点时，另一个点也随之停止运动．在运动过程中，△PCQ关于直线PQ对称的图形是△PDQ．设运动时间为t（秒），是否存在时刻t，使得PD∥AB？若存在，求出t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，AD是△ABC的高，点E、F在BC边上，点G在AC边上，点H在BC边上，BC=21cm，高AD=15cm，四边形EFGH是△ABC内接正方形，
    （1）△AHG与△ABC相似吗？为什么？
    （2）求内接正方形EFGH边长EF．

    查看答案和解析>>

    同步练习册答案