
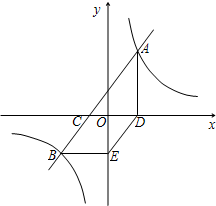 如图,已知直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.
如图,已知直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.分析 (1)根据反比例函数图象上点的坐标特征,将点A代入双曲线方程求得k值,即利用待定系数法求得双曲线方程;然后将B点代入其中,从而求得a值;设直线AB的解析式为y=mx+n,将A、B两点的坐标代入,利用待定系数法解答;
(2)由点C、D的坐标、已知条件“BE∥x轴”及两点间的距离公式求得,CD=5,BE=5,且BE∥CD,从而可以证明四边形CBED是平行四边形;然后在Rt△OED中根据勾股定理求得ED=5,所以ED=CD,从而证明四边形CBED是菱形;
(3)利用函数图象得出一次函数大于反比例函数时x的取值范围.
解答 解:(1)∵双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$),
∴k=20.
把B(-5,a)代入y=$\frac{20}{x}$,得a=-4.
∴点B的坐标是(-5,-4),
设直线AB的解析式为y=mx+n,
将A(3,$\frac{20}{3}$)、B(-5,-4)代入,得$\left\{\begin{array}{l}{\frac{20}{3}=3m+n}\\{-4=-5m+n}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=\frac{4}{3}}\\{n=\frac{8}{3}}\end{array}\right.$,
∴直线AB的解析式为:y=$\frac{4}{3}$x+$\frac{8}{3}$;
(2)四边形CBED是菱形.理由如下:
∵直线AB的解析式为:y=$\frac{4}{3}$x+$\frac{8}{3}$,
∴当y=0时,x=-2,
∴点C的坐标是(-2,0);
∵点D在x轴上,AD⊥x轴,A(3,$\frac{20}{3}$),
∴点D的坐标是(3,0),
∵BE∥x轴,
∴点E的坐标是(0,-4).
而CD=5,BE=5,且BE∥CD.
∴四边形CBED是平行四边形.
在Rt△OED中,ED2=OE2+OD2,
∴ED=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴ED=CD.
∴平行四边形CBED是菱形;
(3)利用图象可得:当直线AB的函数值不大于双曲线的函数值时,自变量x的取值范围为x≤-5或0<x≤3.
点评 此题主要考查了待定系数法求一次函数与反比例的解析式以及菱形的判定与性质等知识,利用数形结合比较得出函数值大小以及结合菱形判定得出是解题关键.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
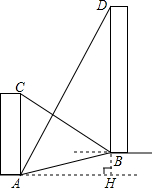 如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是$1:2\sqrt{3}$.从点A测得楼BD顶部D处的仰角是60°,从点B测得楼AC顶部C处的仰角是30°,楼BD的自身高度比楼AC高12m.求楼AC与楼BD之间的水平距离.(结果保留根号)
如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是$1:2\sqrt{3}$.从点A测得楼BD顶部D处的仰角是60°,从点B测得楼AC顶部C处的仰角是30°,楼BD的自身高度比楼AC高12m.求楼AC与楼BD之间的水平距离.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在玲玲家住宅楼CD的前面新建了一个大型商场AB,当光线与地面的夹角是22°时,商场在玲玲家楼上留下高2m的影子CE;而当光线与地面的夹角是45°时,商场楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).求商场AB的高度.(参考数据:sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$)
如图,在玲玲家住宅楼CD的前面新建了一个大型商场AB,当光线与地面的夹角是22°时,商场在玲玲家楼上留下高2m的影子CE;而当光线与地面的夹角是45°时,商场楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).求商场AB的高度.(参考数据:sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com