
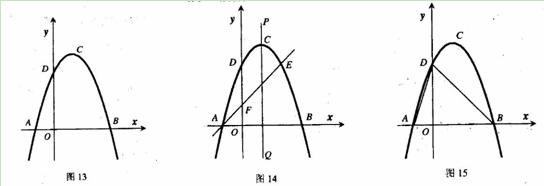
(9分)如图13,抛物线y=ax2+bx+c(a≠0)的顶点为(1,4),交x轴于A、B,交y轴于D,其中B点的坐标为(3,0)
(1)求抛物线的解析式
(2)如图14,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则x轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由.
(3)如图15,抛物线上是否存在一点T,过点T作x的垂线,垂足为M,过点M作直线MN∥BD,交线段AD于点N,连接MD,使△DNM∽△BMD,若存在,求出点T的坐标;若不存在,说明理由.

解:(1)设所求抛物线的解析式为: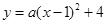 ,依题意,将点B(3,0)代入,得:
,依题意,将点B(3,0)代入,得: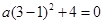 解得:a=-1
解得:a=-1
∴所求抛物线的解析式为:
(2)如图6,在y轴的负半轴上取一点I,使得点F与点I关于x轴对称,

在x轴上取一点H,连接HF、HI、HG、GD、GE,则HF=HI…………………①
设过A、E两点的一次函数解析式为:y=kx+b(k≠0),
∵点E在抛物线上且点E的横坐标为2,将x=2代入抛物线 ,得
,得
∴点E坐标为(2,3)
又∵抛物线 图像分别与x轴、y轴交于点A、B、D
图像分别与x轴、y轴交于点A、B、D
∴当y=0时, ,∴x=-1或x=3
,∴x=-1或x=3
当x=0时,y=-1+4=3,
∴点A(-1,0),点B(3,0),点D(0,3)
又∵抛物线的对称轴为:直线x=1,
∴点D与点E关于PQ对称,GD=GE…………………②
分别将点A(-1,0)、点E(2,3)代入y=kx+b,得:
 解得:
解得: 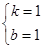
过A、E两点的一次函数解析式为:y=x+1
∴当x=0时,y=1
∴点F坐标为(0,1)
∴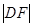 =2………………………………………③
=2………………………………………③
又∵点F与点I关于x轴对称,
∴点I坐标为(0,-1)
∴ ………④
………④
又∵要使四边形DFHG的周长最小,由于DF是一个定值,
∴只要使DG+GH+HI最小即可
由图形的对称性和①、②、③,可知,
DG+GH+HF=EG+GH+HI
只有当EI为一条直线时,EG+GH+HI最小
设过E(2,3)、I(0,-1)两点的函数解析式为: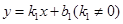 ,
,
分别将点E(2,3)、点I(0,-1)代入 ,得:
,得:
 解得:
解得:
过A、E两点的一次函数解析式为:y=2x-1
∴当x=1时,y=1;当y=0时,x= ;
;
∴点G坐标为(1,1),点H坐标为( ,0)
,0)
∴四边形DFHG的周长最小为:DF+DG+GH+HF=DF+EI
由③和④,可知:
DF+EI=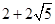
∴四边形DFHG的周长最小为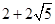 。
。
(3)如图7,由题意可知,∠NMD=∠MDB,
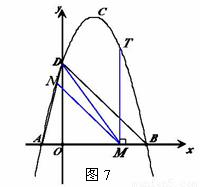
要使,△DNM∽△BMD,只要使 即可,
即可,
即: ………………………………⑤
………………………………⑤
设点M的坐标为(a,0),由MN∥BD,可得 △AMN∽△ABD,
∴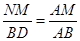
再由(1)、(2)可知,AM=1+a,BD=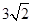 ,AB=4
,AB=4
∴ 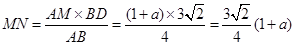
∵ ,
,
∴⑤式可写成:
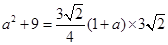
解得: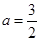 或
或 (不合题意,舍去)
(不合题意,舍去)
∴点M的坐标为(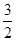 ,0)
,0)
又∵点T在抛物线 图像上,
图像上,
∴当x=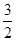 时,y=
时,y=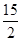
∴点T的坐标为(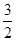 ,
,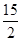 ).
).
【解析】略


科目:初中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 3 |

| 1 |
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
(9分)如图13,抛物线y=ax2+bx+c(a≠0)的顶点为(1,4),交x轴于A、B,交y轴于D,其中B点的坐标为(3,0)
(1)求抛物线的解析式
(2)如图14,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则x轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由.
(3)如图15,抛物线上是否存在一点T,过点T作x的垂线,垂足为M,过点M作直线MN∥BD,交线段AD于点N,连接MD,使△DNM∽△BMD,若存在,求出点T的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(福建洛江区卷)数学 题型:解答题
(9分)如图13,抛物线y=ax2+bx+c(a≠0)的顶点为(1,4),交x轴于A、B,交y轴于D,其中B点的坐标为(3,0)
(1)求抛物线的解析式
(2)如图14,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则x轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由.
(3)如图15,抛物线上是否存在一点T,过点T作x的垂线,垂足为M,过点M作直线MN∥BD,交线段AD于点N,连接MD,使△DNM∽△BMD,若存在,求出点T的坐标;若不存在,说明理由.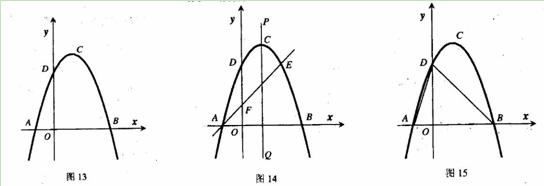
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com