
如图, ABCD的顶点A、B的坐标分别是A(-1,0)B(0,-2),顶点C、D在双曲线
ABCD的顶点A、B的坐标分别是A(-1,0)B(0,-2),顶点C、D在双曲线 上,边AD交y轴于点E,且
上,边AD交y轴于点E,且 ABCD的面积是△ABE面积的8倍,则k= .
ABCD的面积是△ABE面积的8倍,则k= .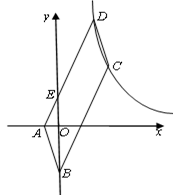
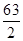 .
.
解析试题分析:分别过C、D作x轴的垂线,垂足为F、G,过C点作CH⊥DG,垂足为H,根据CD∥AB,CD=AB可证△CDH≌△ABO,则CH=AO=1,DH=OB=2,由此设C(m+1,n),D(m,n+2),C、D两点在双曲线 上,则(m+1)n=m(n+2),解得n=2m,设直线AD解析式为y=ax+b,将A、D两点坐标代入求解析式,确定E点坐标,求S△ABE,根据S四边形BCDE=8S△ABE,列方程求m、n的值,根据k=(m+1)n求解.
上,则(m+1)n=m(n+2),解得n=2m,设直线AD解析式为y=ax+b,将A、D两点坐标代入求解析式,确定E点坐标,求S△ABE,根据S四边形BCDE=8S△ABE,列方程求m、n的值,根据k=(m+1)n求解.
试题解析:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,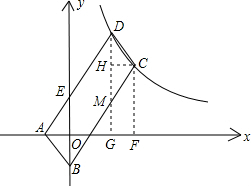
∵ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
∴△CDH≌△ABO(AAS),
∴CH=AO=1,DH=OB=2,设C(m+1,n),D(m,n+2),
则(m+1)n=m(n+2)=k,
解得n=2m,则D的坐标是(m,2m+2),
设直线AD解析式为y=ax+b,将A、D两点坐标代入得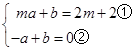 ,
,
由②得:a=b,代入①得:mb+b=2m+2,
即b(m+1)=2(m+1),解得b=2,
则 a=2 , b=2,
∴y=2x+2,E(0,2),BE=4,
∴S△ABE= ×BE×AO=2,
×BE×AO=2,
∵S四边形BCDE=8S△ABE=8× ×4×1=16,
×4×1=16,
∵S四边形BCDE=S△ABE+S四边形BEDM=16,
即2+4×m=16,
解得m=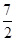 ,
,
∴n=2m=7,
∴k=(m+1)n=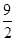 ×7=
×7=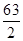 .
.
考点:1.平行四边形的性质;2.反比例函数图象上点的坐标特征.


科目:初中数学 来源: 题型:单选题
如图,Rt△ABC的顶点A在双曲线 的图象上,直角边BC在x轴上,∠ABC=90°,∠ACB=30°,OC=4,连接OA,∠AOB=60°,则k的值是
的图象上,直角边BC在x轴上,∠ABC=90°,∠ACB=30°,OC=4,连接OA,∠AOB=60°,则k的值是
A. | B. | C. | D. |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,点A是反比例函数y=的图象上﹣点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y=的图象于点C,则△OAC的面积为 _________ .
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y= 的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为 .
的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,P1、P2、P3…Pn(n为正整数)分别是反比例函数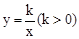 在第一象限图象上的点,A1、A2、A3…An分别为x轴上的点,且△P1OA1、△P2A1A2、△P3A2A3…△PnAn-1An均为等边三角形.若点A1的坐标为(2,0),则点A2的坐标为__________________,点An的坐标为__________________.
在第一象限图象上的点,A1、A2、A3…An分别为x轴上的点,且△P1OA1、△P2A1A2、△P3A2A3…△PnAn-1An均为等边三角形.若点A1的坐标为(2,0),则点A2的坐标为__________________,点An的坐标为__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,函数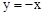 与函数
与函数 的图象相交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,D.则四边形ACBD的面积为
的图象相交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,D.则四边形ACBD的面积为
A.2 B.4 C.6 D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com