
【题目】两个全等的含30°,60°角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.试判断△EMC的形状,并说明理由.
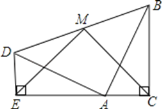
【答案】△EMC是等腰直角三角形,证明见解析
【解析】
欲判断△EMC的形状,需知道其三边关系.根据题意需证EM=CM,由此证明△EMD≌△CMA即可.依据等腰直角三角形性质易证.
解:△EMC是等腰直角三角形.
理由如下:
连接MA.
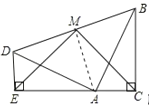
∵∠EAD=30°,∠BAC=60°,∴∠DAB=90°,
∵△EDA≌△CAB,∴DA=AB,ED=AC,
∴△DAB是等腰直角三角形.
∴∠MDA=∠MBA=45°
又∵M为BD的中点,
∴∠MAD=∠MAB=![]() 45°,AM⊥BD(三线合一),
45°,AM⊥BD(三线合一),
∴AM=![]() =MD,
=MD,
∴∠EDM=∠MAC=105°,
在△MDE和△MAC中,
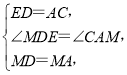
∴△MDE≌△MAC.
∴∠DME=∠AMC,ME=MC,
又∵∠DMA=90°,∴∠EMC=∠EMA+∠AMC=∠EMA+∠DME=∠DMA=90°.
∴△MEC是等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题
(1)画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1,并写出点C1的坐标;
(2)画出将△ABC关于原点O对称的图形△A2B2C2,并写出点C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了____m,恰好把水喷到F处进行灭火.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.当BC的长度变化时,按照同样的放置方式,左上角与右下角的阴影部分的面积的差S始终保持不变,则a,b满足的关系是________________.
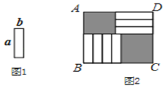
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).


求(1)抛物线的解析式;
(2)两盏景观灯P1、P2之间的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③a-2b+4c<0;④8a+c>0.其中正确的有____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)二次函数的顶点在![]() 轴上,求
轴上,求![]() 的值;
的值;
(2)若二次函数与![]() 轴的两个交点A、B均为整数点(坐标为整数的点),当
轴的两个交点A、B均为整数点(坐标为整数的点),当![]() 为整数时,求A、B两点的坐标.
为整数时,求A、B两点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com