
分析 (1)利用待定系数法即可解决问题.
(2)求出y1,y2,y3代入解方程即可解决问题,注意运算技巧.
(3)当D为直角顶点时,由图象可知不存在点P,使得△PCD为直角三角形,当C为直角顶点,CD为直角边时,作PE⊥OC于E.分两种情形①CD=2PC,②PC=2CD,
设直线y=-2x向下平移m个单位,则直线CD解析式为y=-2x-m,求出点P坐标(用m表示),代入抛物线解析式即可解决问题.
解答 解:(1)把(-1,0)和(2,6)代入y=x2+bx+c中,
得$\left\{\begin{array}{l}{1-b+c=0}\\{4+2b+c=6}\end{array}\right.$解得$\left\{\begin{array}{l}{b=1}\\{c=0}\end{array}\right.$,
∴b=1,c=0.
(2)由题意y1=n2+n,y2=(n+1)2+(n+1),y3=(n+2)2+(n+2),
∵$\frac{1}{{y}_{1}}$+$\frac{1}{{y}_{2}}$+$\frac{1}{{y}_{3}}$=$\frac{3}{10}$,
∴$\frac{1}{n(n+1)}$+$\frac{1}{(n+1)(n+2)}$+$\frac{1}{(n+2)(n+3)}$=$\frac{3}{10}$,
∴$\frac{1}{n}$-$\frac{1}{n+1}$+$\frac{1}{n+1}$-$\frac{1}{n+2}$+$\frac{1}{n+2}$-$\frac{1}{n+3}$=$\frac{3}{10}$,
∴$\frac{1}{n}$-$\frac{1}{n+3}$=$\frac{3}{10}$,
整理得n2+3n-10=0,
解得n=2或-5.
经过检验n=2和-5是分式方程的解.
(3)当D为直角顶点时,由图象可知不存在点P,使得△PCD为直角三角形,当C为直角顶点,CD为直角边时,作PE⊥OC于E.
设直线y=-2x向下平移m个单位,则直线CD解析式为y=-2x-m,
∴点D坐标(0,-m),点C坐标(-$\frac{m}{2}$,0),
∴OD=m,OC=$\frac{m}{2}$,
∴OD=20C,
∵△PCD与△OCD相似,
∴CD=2PC或PC=2CD,
①当CD=2PC时,
∵∠PCD=90°,
∴∠PCE+∠DCO=90°,∠DCO+∠CDO=90°,
∴∠PCE=∠CDO,
∵∠PEC=∠COD=90°,
∴△COD∽△PEC,
∴$\frac{CD}{PC}$=$\frac{OD}{EC}$=$\frac{CO}{PE}$=2,
∴EC=$\frac{m}{2}$,PE=$\frac{m}{4}$,
∴点P坐标(-m,-$\frac{m}{4}$),代入y=x2+x,
得-$\frac{m}{4}$=m2-m,解得m=$\frac{3}{4}$或(0舍弃)
∴点P坐标(-$\frac{3}{4}$,-$\frac{3}{16}$).
②PC=2CD时,由$\frac{CD}{PC}$=$\frac{OD}{EC}$=$\frac{CO}{PE}$=$\frac{1}{2}$,
∴EC=2m,PE=m,
∴点P坐标(-$\frac{5}{2}$m,-m),代入y=x2+x,
得-m=$\frac{25}{4}$m2-$\frac{5}{2}$m,
解得m=$\frac{6}{25}$和(0舍弃),
∴点P坐标(-$\frac{3}{5}$,-$\frac{6}{25}$).
点评 本题考查二次函数综合题、分式方程、相似三角形的判定和性质、一次函数等知识,解题的关键是灵活掌握待定系数法,学会用参数解决问题,学会分类讨论,不能漏解,属于中考压轴题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:选择题
| A. | 打开电视,正在播放《大国工匠》 | |
| B. | 袋中只有10个球,且都是红球,任意摸出一个球是红球 | |
| C. | 5年后数学课代表会考上清华大学 | |
| D. | 2015年全年由367天 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
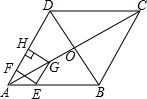 如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒
如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒查看答案和解析>>
科目:初中数学 来源: 题型:解答题
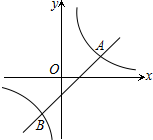 如图,已知A(4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点
如图,已知A(4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 型号 | A | B | C | D | E |
| 数量(双) | 3 | 8 | 22 | 10 | 4 |
| A. | 众数 | B. | 平均数 | C. | 中位数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
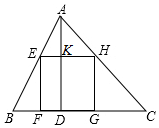 若正方形有两个相邻顶点在三角形的同一条边上,其余两个顶点分别在三角形的另两条边上,则正方形称为三角形该边上的内接正方形,△ABC中,设BC=a,AC=b,AB=c,各边上的高分别记为ha,hb,hc,各边上的内接正方形的边长分别记为xa,xb,xc
若正方形有两个相邻顶点在三角形的同一条边上,其余两个顶点分别在三角形的另两条边上,则正方形称为三角形该边上的内接正方形,△ABC中,设BC=a,AC=b,AB=c,各边上的高分别记为ha,hb,hc,各边上的内接正方形的边长分别记为xa,xb,xc查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8cm | B. | 84m | C. | 8cm或4cm | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
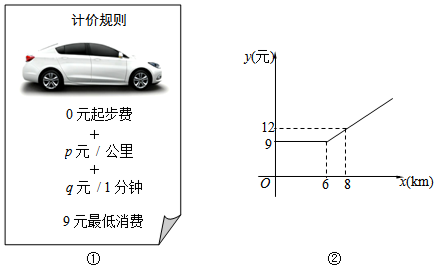
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com