
����Ŀ����ͼ��AB�ǡ�O��ֱ����AC���ң� 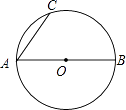
��1�����㰴���沽�軭ͼ����ͼ����������ʱ��ʹ��Ǧ�ʻ�����ȷ�������ʹ�ú�ɫ�ּ���ǩ�ֱ���ڣ��� ��һ��������A����BAC�Ľ�ƽ���ߣ�����O�ڵ�D��
�ڶ���������D��AC�Ĵ��ߣ���AC���ӳ����ڵ�E��
������������BD��
��2����֤��AD2=AEAB��
��3������EO����AD�ڵ�F����5AC=3AB���� ![]() ��ֵ��
��ֵ��
���𰸡�
��1���⣺��ͼ��
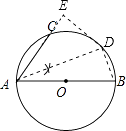
��2��֤������AB�ǡ�O��ֱ����
���ADB=90�㣬
��DE��AC��
���AED=90�㣬
��ADƽ�֡�CAB��
���CAD=��DAB��
��Rt��ADE��Rt��ABD��
��AD��AB=AE��AD��
��AD2=AEAB��
��3���⣺��OD��BC�����ǽ��ڵ�G����ͼ��
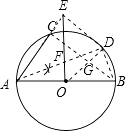
��5AC=3AB����AC��AB=3��5��
�����AC=3x��AB=5x��
��AB�ǡ�O��ֱ����
���ACB=90�㣬
�֡ߡ�CAD=��DAB��
�DC=��DB��
��OD��ֱƽ��BC��
��OD��AE��
��OG= ![]() AC=
AC= ![]() x����AED=90�㣬
x����AED=90�㣬
���ı���ECGDΪ���Σ�
��CE=DG=OD��OG= ![]() x��
x�� ![]() x=x��
x=x��
��AE=AC+CE=3x+x=4x��
��AE��OD��
���AEF�ס�DOF��
��AE��OD=EF��OF��
��EF��OF=4x�� ![]() x=8��5��
x=8��5��
�� ![]() ��
��
����������1�����ݻ�����ͼ������BAC�Ľ�ƽ����AD����O�ڵ�D����D��AC�Ĵ��ߣ�����Ϊ��E����2������ֱ�����Ե�Բ�ܽ�Ϊֱ�ǵõ���ADB=90�㣬��DE��AC�����AED=90�㣬����ADƽ�֡�CAB�õ���CAD=��DAB���������������ε��ж��õ�Rt��ADE��Rt��ABD���������Ƶ����ʵõ�AD��AB=AE��AD�����ñ��������ʼ��ɵõ�AD2=AEAB����3����OD��BC�����ǽ��ڵ�G����5AC=3AB������AC=3x��AB=5x������ֱ�����Ե�Բ�ܽ�Ϊֱ�ǵõ���ACB=90�㣬�ɡ�CAD=��DAB�õ���DC=��DB�����ݴ������������۵õ�OD��ֱƽ��BC������OD��AE��OG= ![]() AC=
AC= ![]() x�����ҵõ��ı���ECGDΪ���Σ���CE=DG=OD��OG=
x�����ҵõ��ı���ECGDΪ���Σ���CE=DG=OD��OG= ![]() x��
x�� ![]() x=x���ɼ����AE=AC+CE=3x+x=4x������AE��OD�ɵõ���AEF�ס�DOF����AE��OD=EF��OF����EF��OF=4x��
x=x���ɼ����AE=AC+CE=3x+x=4x������AE��OD�ɵõ���AEF�ס�DOF����AE��OD=EF��OF����EF��OF=4x�� ![]() x=8��5��Ȼ����ݱ��������ʼ��ɵõ�
x=8��5��Ȼ����ݱ��������ʼ��ɵõ� ![]() ��ֵ��
��ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB=AC=AD����CAD=60�����ֱ�����BC��BD����AEƽ�֡�BAC��BD�ڵ�E����BE=4��ED=8����DF=_____��
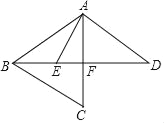
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+12x��30�Ķ���ΪA���Գ���AB��x�ύ�ڵ�B����x�Ϸ�������������C��D���㣬���ǹ���AB�Գƣ�����C���ڶԳ������࣬CB��DB��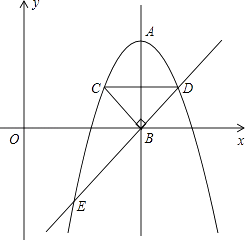
��1������������ߵĶԳ���Ͷ���A�����ꣻ
��2���������ߵĶԳ������ҳ���Q��ʹ����A��C����ľ�����ȣ��������Q�����ꣻ
��3���ӳ�DB���������ڵ�E�������������Ƿ���ڵ�P��ʹ�á�DEP��������ڡ�DEC������������ڣ�����ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
��ʾ��������y=ax2+bx+c��a��0���ĶԳ���Ϊ ![]() ����������Ϊ
����������Ϊ ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����M��N�ֱ���AB��AC�ϵĵ㣬��AM=AN������MN��CM��BN����D��E��F��G�ֱ���BC��MN��BN��CM���е㣬����E��F��D��G��
��l���ж��ı���EFDG����״���� ��������֤������
��2���ֽ���AMN�Ƶ�A��תһ���ĽǶȣ������������䣨��ͼ�ڣ����ı���EFDG����״�Ƿ����仯��֤����Ľ��ۣ�
��3����ͼ�ڣ��ڣ�2��������£��뽫��ABC��ԭ�е�����������һ��������ʹ�ı���EFDG�������Σ���д�������ӵ��������������������Ļ�����֤���ı���EFDG�������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и�����Ҫ����࣮
��2��5��![]() ��0����3.4����21����
��0����3.4����21����![]() ��3.7��15%��
��3.7��15%��
�������ϣ�{_____��}��
���������ϣ�{_____��}��
�������ϣ�{_____��}
���������ϣ�{_____��}
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCΪ�ȱ������Σ�D��E�ֱ���AC��BC�ϵĵ㣬��AD=CE��AE��BD�ཻ�ڵ�P��BF��AE�ڵ�F����BP=4����PF�ij��� ��
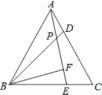
A. 2 B. 3 C. 1 D. 8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���AB�Ĵ�ֱƽ������Խ���AC�ཻ�ڵ�E����ABC=140�㣬��ô��EDC= �� 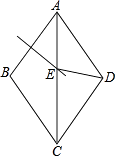
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ4��������ABCD�У�����P��A���������ÿ��1����λ���ȵ��ٶ���AB��B���˶���ͬʱ����Q��B���������ÿ��2����λ���ȵ��ٶ���BC��CD�����˶�����P�˶���B��ʱ��P��Q����ͬʱֹͣ�˶�����P���˶���ʱ��Ϊt����APQ�����ΪS����S��t�ĺ�����ϵ��ͼ���ǣ�������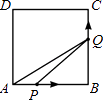
A.
B.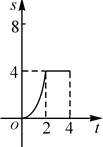
C.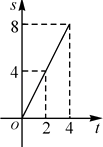
D.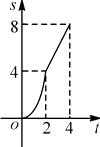
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com