
 如图,气象大厦离小伟家80米,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是42°,而大厦底部的俯角是34°,求该大厦的高度(结果精确到0.1米)
如图,气象大厦离小伟家80米,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是42°,而大厦底部的俯角是34°,求该大厦的高度(结果精确到0.1米)分析 首先过点A作AE⊥BC于E,可得四边形ADCE是矩形,即可得DC=AE=80米,然后分别在Rt△ACE中,EC=80×tan34°与在Rt△ABE中,BE=AE•tan42°,即可求得BE的长,继而求得电梯楼的高度.
解答  解:过点A作AE⊥BC于E,
解:过点A作AE⊥BC于E,
∵AD⊥CD,BC⊥CD,
∴四边形ADCE是矩形,
∵CD=80米,
∴EC=80×tan34°=53.6米,
在Rt△ABE中,BE=AE•tan42°=72(米),
∴BC=CE+BE=53.6+72=125.6(米).
答:电梯楼的高度BC为125.6米
点评 此题考查了仰角与俯角的知识.此题难度适中,注意能借助仰角或俯角构造直角三角形并解直角三角形是解此题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 80 | B. | 100 | C. | 120 | D. | 160 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $(3-2\sqrt{3})(3+2\sqrt{3})={3^2}$-2×3=3 | B. | $(2\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})=2a-b$ | ||
| C. | ${(3-2\sqrt{3})^2}={3^2}-{(2\sqrt{3})^2}$=9-12=-3 | D. | $(\sqrt{a}+\sqrt{a-1})(\sqrt{a}-\sqrt{a-1})={(\sqrt{a})^2}-{(\sqrt{a-1})^2}$=a-(a-1)=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
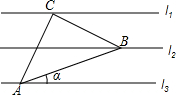 已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个项点分别在这三条平行直线上,则sinα的值是$\frac{\sqrt{10}}{10}$.
已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个项点分别在这三条平行直线上,则sinα的值是$\frac{\sqrt{10}}{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 国家食品药品监督管理局对某品牌火腿抽检中,有四包真空小包装火腿,每包以标准克数(450g)为基准,超过的克数记作正数,不足的克数记作负数,以下数据是记录结果,其中表示实际克数最接近标准克数的是( )
国家食品药品监督管理局对某品牌火腿抽检中,有四包真空小包装火腿,每包以标准克数(450g)为基准,超过的克数记作正数,不足的克数记作负数,以下数据是记录结果,其中表示实际克数最接近标准克数的是( )| A. | +2 | B. | -3 | C. | +3 | D. | +4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com