
【题目】如图,分别以线段AC的两个端点A,C为圆心,大于![]() AC的长为半径画弧,两弧相交于B,D两点,连接BD,AB,BC,CD,DA,以下结论:
AC的长为半径画弧,两弧相交于B,D两点,连接BD,AB,BC,CD,DA,以下结论:
①BD垂直平分AC;
②AC平分∠BAD;
③AC=BD;
④四边形ABCD是中心对称图形.
其中正确的有( )
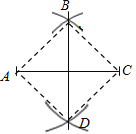
A. ①②③ B. ①③④ C. ①②④ D. ②③④
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
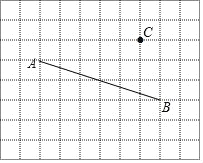
【题目】利用网格画图:
(1)过点C画AB的平行线;
(2)过点C画AB的垂线,垂足为E;
(3)连接CA、CB,在线段CA、CB、CE中, 线段最短,理由: ;
(4)点C到直线AB的距离是线段的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨![]() 元收费
元收费![]() 如果超过20吨,未超过的部分按每吨
如果超过20吨,未超过的部分按每吨![]() 元收费,超过的部分按每吨
元收费,超过的部分按每吨![]() 元收费
元收费![]() 设某户每月用水量为x吨,应收水费为y元.
设某户每月用水量为x吨,应收水费为y元.
![]() 设某户居民每月用水量为m吨
设某户居民每月用水量为m吨![]() ,则应收水费为______元
,则应收水费为______元![]() 用含m的代数式表示
用含m的代数式表示![]() ;
;
![]() 设某户居民每月用水量为m吨
设某户居民每月用水量为m吨![]() ,则应收水费为______元
,则应收水费为______元![]() 用含m的代数式表示
用含m的代数式表示![]() ;
;
![]() 若该城市某户5月份水费平均为每吨
若该城市某户5月份水费平均为每吨![]() 元,求该户5月份用水多少吨?
元,求该户5月份用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD内放入六个小正方形后形成一个中心对称图形,其中顶点E、F分别在边BC、AD上,则长AD与宽AB的比值为( )
A.6:5
B.13:10
C.8:7
D.4:3
查看答案和解析>>
科目:初中数学 来源: 题型:
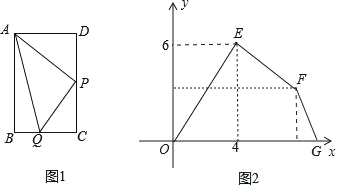
【题目】如图1,在长方形ABCD中,点P是CD中点,点Q从点A开始,沿着A→B→C→P的路线匀速运动,设△APQ的面积是y,点Q经过的路线长度为x,图2坐标系中折线OEFG表示y与x之间的函数关系,点E的坐标为(4,6),则点G的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和爸爸周末步行去游泳馆游冰,爸爸先出发了一段时间后小明才出发,途中小明在离家1400米处的报亭休息了一段时间后继续按原来的速度前往游泳馆.两人离家的距离y(米)与小明所走时间x(分钟)之间的函数关系如图所示,请结合图象信息解答下列问题:
(1)小明出发 分钟后第一次与爸爸相遇;
(2)分别求出爸爸离家的距离y1和小明到达报亭前离家的距离y2与时间x之间的函数关系式;
(3)求小明在报亭休息了多长时间遇到姗姗来迟的爸爸;
(4)若游泳馆离小明家2000米,请你通过计算说明谁先到达游泳馆.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2014年12月28日北京公交地铁调价以来,人们的出行成本发生了较大的变化. 小林根据新闻,将地铁和公交车的票价绘制成了如下两个表格。(说明:表格中“6~12公里”指的是大于6公里,小于等于12公里,其他类似)
|
| ||||||||||||||||||||||||||||||
根据以上信息回答下列问题:
小林办了一张市政交通一卡通学生卡,目前乘坐地铁没有折扣。
(1)如果小林全程乘坐地铁的里程为14公里,用他的学生卡需要刷卡交费________元;
(2)如果小林全程乘坐公交车的里程为16公里,用他的学生卡需要刷卡交________元;
(3)小林用他的学生卡乘坐一段地铁后换乘公交车,两者累计里程为12公里。已知他乘坐地铁平均每公里花费0.4元,乘坐公交车平均每公里花费0.25元,此次行程共花费4.5元。请问小林乘坐地铁和公交车的里程分别是多少公里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 分别交x轴、y轴于A、B两点,点P是线段AB上的一动点,以P为圆心,r为半径画圆.
分别交x轴、y轴于A、B两点,点P是线段AB上的一动点,以P为圆心,r为半径画圆.
(1)若点P的横坐标为﹣3,当⊙P与x轴相切时,则半径r为 ,此时⊙P与y轴的位置关系是 .(直接写结果)
(2)若![]() ,当⊙P与坐标轴有且只有3个公共点时,求点P的坐标.
,当⊙P与坐标轴有且只有3个公共点时,求点P的坐标.
(3)如图2,当圆心P与A重合,![]() 时,设点C为⊙P上的一个动点,连接OC,将线段OC绕点O顺时针旋转90°,得到线段OD,连接AD,求AD长的最值并直接写出对应的点D的坐标.
时,设点C为⊙P上的一个动点,连接OC,将线段OC绕点O顺时针旋转90°,得到线段OD,连接AD,求AD长的最值并直接写出对应的点D的坐标.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com