
”¾ĢāÄæ”æijĢģŌē³æ£¬ÕÅĒæ“Ó¼ŅÅܲ½Č„ĢåÓż¶ĶĮ¶£¬Ķ¬Ź±ĀčĀč“ÓĢåÓż³”³æĮ·½įŹų»Ų¼Ņ£¬Ķ¾ÖŠĮ½ČĖĻąÓö£¬ÕÅĒæÅܵ½ĢåÓż³”ŗó·¢ĻÖŅŖĻĀÓź£¬Į¢¼“°“ŌĀ··µ»Ų£¬Óöµ½ĀčĀčŗóĮ½ČĖŅ»Ęš»Ųµ½¼Ņ£ØÕÅĒæŗĶĀčĀčŹ¼ÖÕŌŚĶ¬Ņ»Ģõ±ŹÖ±µÄ¹«Ā·ÉĻŠŠ×ߣ©£®ČēĶ¼ŹĒĮ½ČĖĄė¼ŅµÄ¾ąĄėy£ØĆ×£©ÓėÕÅĒæ³ö·¢µÄŹ±¼äx£Ø·Ö£©Ö®¼äµÄŗÆŹżĶ¼Ļó£¬øł¾ŻĶ¼ĻóŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ĒóÕÅĒæ·µ»ŲŹ±µÄĖŁ¶Č£»
£Ø2£©ĀčĀč±Č°“ŌĖŁ·µ»ŲĢįĒ°¶ąÉŁ·ÖÖÓµ½¼Ņ£æ
£Ø3£©ĒėÖ±½ÓŠ“³öÕÅĒæÓėĀčĀčŗĪŹ±Ļą¾ą1200Ć×£æ

”¾“š°ø”æ£Ø1£©150Ć×/·Ö£»£Ø2£©10·ÖÖÓ£»£Ø3£©12·Ö£¬28·Ö£¬33·Ö.
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©øł¾ŻĖŁ¶Č=Ā·³Ģ”ĀŹ±¼ä£¬¼“æɽā“š£»£Ø2£©Ēó³öĀčĀčŌĄ“µÄĖŁ¶Č£¬ĀčĀčŌĄ“×ßĶź3000Ć×ĖłÓƵď±¼ä£¬¼“æɽā“š£»£Ø3£©·Ö±šĒó³öÕÅĒæŗĶĀčĀčµÄŗÆŹż½āĪöŹ½£¬øł¾ŻÕÅĒæÓėĀčĀčĻą¾ą1000Ć×£¬ĮŠ³ö·½³Ģ£¬¼“æɽā“š£®
ŹŌĢā½āĪö£ŗ(1)3000”Ā(5030)=3000”Ā20=150(Ć×/·Ö)£¬
“š£ŗÕÅĒæ·µ»ŲŹ±µÄĖŁ¶ČĪŖ150Ć×/·Ö£»
(2)(4530)”Į150=2250(Ć×),µćBµÄ×ų±źĪŖ(45,750)£¬
ĀčĀčŌĄ“µÄĖŁ¶ČĪŖ£ŗ2250”Ā45=50(Ć×/·Ö)£¬
ĀčĀčŌĄ“»Ų¼ŅĖłÓƵď±¼äĪŖ£ŗ3000”Ā50=60(·Ö)£¬
6050=10(·Ö)£¬
ĀčĀč±Č°“ŌĖŁ·µ»ŲĢįĒ°10·ÖÖÓµ½¼Ņ£»
(3)ČēĶ¼£ŗ
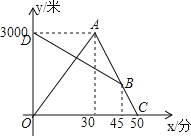
ÉčĻ߶ĪBDµÄŗÆŹż½āĪöŹ½ĪŖ£ŗy=kx+b£¬
°Ń(0,3000),(45,750)“śČėµĆ£ŗ ![]() £¬
£¬
½āµĆ£ŗ ![]() £¬
£¬
”ąy=50x+3000£¬
Ļ߶ĪOAµÄŗÆŹż½āĪöŹ½ĪŖ£ŗy=100x(0x30)£¬
ÉčĻ߶ĪACµÄ½āĪöŹ½ĪŖ£ŗy=k1x+b1£¬
°Ń(30,3000),(50,0)“śČėµĆ£ŗ ![]() £¬
£¬
½āµĆ£ŗ ![]() £¬
£¬
”ąy=150x+7500,(30<x50)
µ±ÕÅĒæÓėĀčĀčĻą¾ą1000Ć׏±,¼“50x+3000100x=1000»ņ100x(50x+3000)=1000»ņ(150x+7500)(50x+3000)=1000£¬
½āµĆ£ŗx=35»ņx=![]() »ņx=
»ņx=![]() £¬
£¬
”ąµ±Ź±¼äĪŖ35·Ö»ņ![]() ·Ö»ņ
·Ö»ņ![]() ·ÖŹ±£¬ÕÅĒæÓėĀčĀčŗĪŹ±Ļą¾ą1000Ć×”£
·ÖŹ±£¬ÕÅĒæÓėĀčĀčŗĪŹ±Ļą¾ą1000Ć×”£


 ŹżŃ§°ĀČüŹī¼ŁĢģĢģĮ·ÄĻ¾©“óѧ³ö°ęÉēĻµĮŠ“š°ø
ŹżŃ§°ĀČüŹī¼ŁĢģĢģĮ·ÄĻ¾©“óѧ³ö°ęÉēĻµĮŠ“š°ø ÄĻ“ó½ĢøØĒĄĻČĘšÅÜŹī¼ŁĻĪ½Ó½Ģ³ĢÄĻ¾©“óѧ³ö°ęÉēĻµĮŠ“š°ø
ÄĻ“ó½ĢøØĒĄĻČĘšÅÜŹī¼ŁĻĪ½Ó½Ģ³ĢÄĻ¾©“óѧ³ö°ęÉēĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅŌŚ400Ć×µÄÖ±ĻßÅܵĄÉĻ“ÓĶ¬Ņ»µŲµćĶ¬ĻņŌČĖŁÅܲ½£¬Ļȵ½ÖÕµćµÄČĖŌµŲŠŻĻ¢£®ŅŃÖŖ¼×ĻČ³ö·¢3Ćė£¬Åܲ½¹ż³ĢÖŠĮ½ČĖµÄ¾ąĄėy£ØĆ×£©ÓėŅŅ³ö·¢µÄŹ±¼ät£ØĆė£©Ö®¼äµÄ¹ŲĻµČēĶ¼ĖłŹ¾£¬ŌņĻĀĮŠ½įĀŪÕżČ·µÄŹĒ£Ø £©
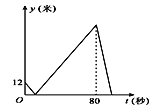
A. ŅŅµÄĖŁ¶ČŹĒ4Ć×/Ćė
B. ĄėæŖĘšµćŗ󣬼ה¢ŅŅĮ½ČĖµŚŅ»“ĪĻąÓöŹ±£¬¾ąĄėĘšµć12Ć×
C. ¼×“ÓĘšµćµ½ÖÕµć¹²ÓĆŹ±83Ćė
D. ŅŅµ½“ļÖÕµćŹ±£¬¼×”¢ŅŅĮ½ČĖĻą¾ą68Ć×
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢĘ·½ų»õµ„¼ŪĪŖ30ŌŖ£¬°“40ŌŖŅ»øöĻśŹŪÄÜĀō40øö£»ČōĻśŹŪµ„¼ŪĆæÕĒ1ŌŖ£¬ŌņĻśĮæ¼õÉŁ1øö£®ĪŖĮĖ»ńµĆ×ī“óĄūČ󣬓ĖÉĢĘ·µÄ×ī¼ŃŹŪ¼ŪÓ¦ĪŖ__ŌŖ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĀņµ„¼ŪĪŖaŌŖµÄĢåĪĀ¼Ęnøö£¬ø¶³öbŌŖ£¬Ó¦ÕŅ»ŲµÄĒ®ŹżŹĒ(””””)
A. (b£na)ŌŖ B. (b£n)ŌŖ C. (na£b)ŌŖ D. (b£a)ŌŖ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¾ŲŠĪ![]() ÖŠ£¬
ÖŠ£¬ ![]() £¬ŅŌ
£¬ŅŌ![]() ĪŖ±ßĻņÉĻ×÷Õż
ĪŖ±ßĻņÉĻ×÷Õż![]() ,
, ![]() Ӣ
”¢![]() ·Ö±š½»
·Ö±š½»![]() ÓŚ
ÓŚ![]() ”¢
”¢![]() £¬
£¬ ![]() £¬Į½¶Æµć
£¬Į½¶Æµć![]() ”¢
”¢![]() ŌĖ¶ÆĖŁ¶Č·Ö±šĪŖ4
ŌĖ¶ÆĖŁ¶Č·Ö±šĪŖ4![]() ”¢
Ӣ![]() (
(![]() ).
).
£Ø1£©![]() µÄ³¤ĪŖ
µÄ³¤ĪŖ ![]() £»
£»
£Ø2£©Čōµć![]() “Ó
“Ó![]() ³ö·¢ŃŲĻ߶Ī
³ö·¢ŃŲĻ߶Ī![]() Ļņ
Ļņ![]() ŌĖ¶Æ£¬Ķ¬Ź±µć
ŌĖ¶Æ£¬Ķ¬Ź±µć![]() “Ó
“Ó![]() ³ö·¢ŃŲĻ߶Ī
³ö·¢ŃŲĻ߶Ī![]() Ļņµć
Ļņµć![]() ŌĖ¶Æ£¬ÉčŌĖ¶ÆŹ±¼äĪŖ
ŌĖ¶Æ£¬ÉčŌĖ¶ÆŹ±¼äĪŖ![]() £¬ŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬ŅŌ
£¬ŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬ŅŌ![]() ”¢
Ӣ![]() Ӣ
”¢![]() ĪŖ¶„µćµÄČż½ĒŠĪŗĶŅŌ
ĪŖ¶„µćµÄČż½ĒŠĪŗĶŅŌ![]() ”¢
Ӣ![]() Ӣ
”¢![]() ĪŖ¶„µćµÄČż½ĒŠĪČ«µČ£¬Ēó
ĪŖ¶„µćµÄČż½ĒŠĪČ«µČ£¬Ēó![]() µÄŌĖ¶ÆĖŁ¶Č
µÄŌĖ¶ÆĖŁ¶Č![]() £»
£»
£Ø3£©Čōµć![]() ŅŌ£Ø2£©ÖŠµÄĖŁ¶Č“Óµć
ŅŌ£Ø2£©ÖŠµÄĖŁ¶Č“Óµć![]() ³ö·¢£¬Ķ¬Ź±µć
³ö·¢£¬Ķ¬Ź±µć![]() ŅŌŌĄ“µÄĖŁ¶Č“Óµć
ŅŌŌĄ“µÄĖŁ¶Č“Óµć![]() ³ö·¢£¬ÄꏱÕėŃŲĖıߊĪ
³ö·¢£¬ÄꏱÕėŃŲĖıߊĪ![]() ŌĖ¶Æ£®ĪŹ
ŌĖ¶Æ£®ĪŹ![]() ”¢
”¢![]() »į²»»įĻąÓö£æČō²»ĻąÓö£¬ĖµĆ÷ĄķÓÉ£®ČōĻąÓö£¬ĒėĒó³ö¾¹ż¶ą³¤Ź±¼ä
»į²»»įĻąÓö£æČō²»ĻąÓö£¬ĖµĆ÷ĄķÓÉ£®ČōĻąÓö£¬ĒėĒó³ö¾¹ż¶ą³¤Ź±¼ä![]() ”¢
”¢![]() µŚŅ»“ĪŌŚĖıߊĪ
µŚŅ»“ĪŌŚĖıߊĪ![]() µÄŗĪ“¦ĻąÓö£æ
µÄŗĪ“¦ĻąÓö£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”涞“ĪŗÆŹży=ax2+bx+c£Øa”Ł0£©µÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬ĻĀĮŠ½įĀŪ£ŗ
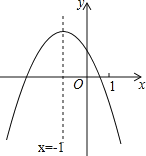
¢Łb2©4ac£¾0£»
¢Ś4a+c£¾2b£»
¢Ū£Øa+c£©2£¾b2£»
¢Üx£Øax+b£©”Üa©b£®
ĘäÖŠÕżČ·½įĀŪµÄŹĒ £®£ØĒė°ŃÕżČ·½įĀŪµÄŠņŗŶ¼ĢīŌŚŗįĻßÉĻ£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
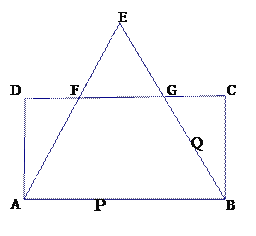
”¾ĢāÄæ”æČēĶ¼1£¬Į½øöµČŃüÖ±½ĒČż½Ē°åABCŗĶDEFÓŠŅ»Ģõ±ßŌŚĶ¬Ņ»ĢõÖ±ĻßlÉĻ£¬DE=2£¬AB=1£®½«Ö±ĻßEBČʵćEÄꏱÕėŠż×Ŗ45”ć£¬½»Ö±ĻßADÓŚµćM£®½«Ķ¼1ÖŠµÄČż½Ē°åABCŃŲÖ±ĻßlĻņÓŅĘ½ŅĘ£¬ÉčC”¢EĮ½µć¼äµÄ¾ąĄėĪŖk£®
½ā“šĪŹĢā£ŗ
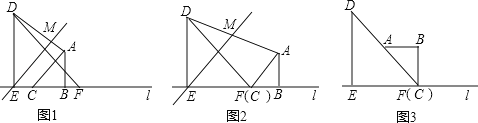
£Ø1£©¢Łµ±µćCÓėµćFÖŲŗĻŹ±£¬ČēĶ¼2ĖłŹ¾£¬æɵĆ![]() µÄÖµĪŖ £»
µÄÖµĪŖ £»
¢ŚŌŚĘ½ŅĘ¹ż³ĢÖŠ£¬![]() µÄÖµĪŖ £ØÓĆŗ¬kµÄ“śŹżŹ½±ķŹ¾£©£»
µÄÖµĪŖ £ØÓĆŗ¬kµÄ“śŹżŹ½±ķŹ¾£©£»
£Ø2£©½«Ķ¼2ÖŠµÄČż½Ē°åABCČʵćCÄꏱÕėŠż×Ŗ£¬ŌĢāÖŠµÄĘäĖūĢõ¼ž±£³Ö²»±ä£®µ±µćAĀäŌŚĻ߶ĪDFÉĻŹ±£¬ČēĶ¼3ĖłŹ¾£¬Ēė²¹Č«Ķ¼ŠĪ£¬¼ĘĖć![]() µÄÖµ£»
掙术
£Ø3£©½«Ķ¼1ÖŠµÄČż½Ē°åABCČʵćCÄꏱÕėŠż×Ŗ¦Į¶Č£¬0£¼¦Į”Ü90£¬ŌĢāÖŠµÄĘäĖūĢõ¼ž±£³Ö²»±ä£®¼ĘĖć![]() µÄÖµ£ØÓĆŗ¬kµÄ“śŹżŹ½±ķŹ¾£©£®
µÄÖµ£ØÓĆŗ¬kµÄ“śŹżŹ½±ķŹ¾£©£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖ½āĶāĄ“Īń¹¤×ÓÅ®¾ĶѧĒéæö£¬Ä³Š£¶ŌĘßÄź¼¶ø÷°ą¼¶ĶāĄ“Īń¹¤×ÓÅ®µÄČĖŹżĒéæö½ųŠŠĮĖĶ³¼Ę£¬·¢ĻÖø÷°ą¼¶ÖŠĶāĄ“Īń¹¤×ÓÅ®µÄČĖŹżÓŠ1Ćū”¢2Ćū”¢3Ćū”¢4Ćū”¢5Ćū”¢6Ćū¹²ĮłÖÖĒéæö£¬²¢ÖĘ³ÉČēĻĀĮ½·łĶ³¼ĘĶ¼£ŗ
(1)ĒóøĆŠ£ĘßÄź¼¶Ę½¾łĆæøö°ą¼¶ÓŠ¶ąÉŁĆūĶāĄ“Īń¹¤×ÓÅ®?²¢½«øĆĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
(2)ѧŠ£¾ö¶Ø“ÓÖ»ÓŠ2ĆūĶāĄ“Īń¹¤×ÓÅ®µÄÕāŠ©°ą¼¶ÖŠ£¬ČĪŃ”Į½Ćū½ųŠŠÉś»ī׏֜£¬ĒėÓĆĮŠ±ķ·Ø»ņ»Ź÷דĶ¼µÄ·½·Ø£¬Ēó³öĖłŃ”Į½ĆūĶāĄ“Īń¹¤×ÓÅ®Ą“×ŌĶ¬Ņ»øö°ą¼¶µÄøÅĀŹ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABĪŖ”ŃOÖ±¾¶£¬EĪŖ”ŃOÉĻŅ»µć£¬”ĻEABµÄĘ½·ÖĻßAC½»”ŃOÓŚCµć£¬¹żCµć×÷CD”ĶAEµÄŃÓ³¤ĻßÓŚDµć£¬Ö±ĻßCDÓėÉäĻßAB½»ÓŚPµć£®
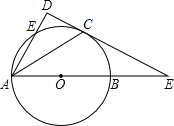
£Ø1£©ĒóÖ¤£ŗDCĪŖ”ŃOĒŠĻߣ»
£Ø2£©ČōDC=1£¬AC=![]() £¬¢ŁĒó”ŃO°ė¾¶³¤£»¢ŚĒóPBµÄ³¤£®
£¬¢ŁĒó”ŃO°ė¾¶³¤£»¢ŚĒóPBµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com