
【题目】如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌![]() ,△AEB≌
,△AEB≌![]() ,且
,且![]() ,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )

A.105°B.100°C.110°D.115°
【答案】B
【解析】
延长C′D交AB′于H.利用全等三角形的性质,平行线的性质,三角形的外角的性质证明∠BFC=∠C′+∠AHC′+∠CAD,再求出∠C′+∠AHC′即可解决问题.
解:延长C′D交AB′于H.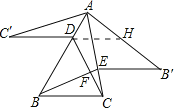
∵△AEB≌△AEB′,
∴∠ABE=∠B′,∠EAB=∠EAB′=40°,
∵C′H∥EB′,
∴∠AHC′=∠B′,
∵△ADC≌△ADC′,
∴∠C′=∠ACD,∠DAC=∠DAC′=40°,
∵∠BFC=∠DBF+∠BDF,∠BDF=∠CAD+∠ACD,
∴∠BFC=∠AHC′+∠C′+∠CAD,
∵∠DAC=∠DAC′=∠CAB′=40°,
∴∠C′AH=120°,
∴∠C′+∠AHC′=60°,
∴∠BFC=60°+40°=100°,
故选:B.


科目:初中数学 来源: 题型:
【题目】兴隆商场用36万元购进A、B两种品牌的服装,销售完后共获利6万元,其进价和售价如下表:

该商场购进A、B两种服装各多少件?
(2)第二次以原价购进A、B两种服装,购进B服装的件数不变,购进A服装的件数是第一次的2倍,A种服装按原价出售,而B种服装打折销售;若两种服装销售完毕,要使第二次销售活动获利不少于81600元,则B种服装最低打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB丄CD于点E,且AB = CD = AC,若点I是三角形ACE的角平分线的交点,点F是BD的中点.下列结论:①∠AIC= 135°;②BD = BI,③S△AIC = S△BID ;④IF⊥AC.其中正确的是_________(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织![]() 名同学和
名同学和![]() 名教师参加校外学习交流活动现打算选租大、小两种客车,大客车载客量为
名教师参加校外学习交流活动现打算选租大、小两种客车,大客车载客量为![]() 人/辆,小客车载客量为
人/辆,小客车载客量为![]() 人/辆
人/辆
(1)学校准备租用![]() 辆客车,有几种租车方案?
辆客车,有几种租车方案?
(2)在(1)的条件下,若大客车租金为![]() 元/辆,小客车租金为
元/辆,小客车租金为![]() 元/辆,哪种租车方案最省钱?
元/辆,哪种租车方案最省钱?
(3)学校临时增加![]() 名学生和
名学生和![]() 名教师参加活动,每辆大客车有2名教师带队,每辆小客车至少有
名教师参加活动,每辆大客车有2名教师带队,每辆小客车至少有![]() 名教师带队.同学先坐满大客车,再依次坐满小客车,最后一辆小客车至少要有
名教师带队.同学先坐满大客车,再依次坐满小客车,最后一辆小客车至少要有![]() 人,请你帮助设计租车方案
人,请你帮助设计租车方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 上的图象经过点
上的图象经过点![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 在第二、四象限分别相交于P、Q两点,与x轴、y轴分别相交于C,D两点
在第二、四象限分别相交于P、Q两点,与x轴、y轴分别相交于C,D两点
![]() 求k的值;
求k的值;
![]() 连接OQ,是否存在实数b,使得
连接OQ,是否存在实数b,使得![]() ?若存在,请求出b的值;若不存在,请说明理由.
?若存在,请求出b的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB、CD相交于点O,若BE平分∠ABD交CD于F,CE平分∠ACD交AB于G,∠A=45°,∠BEC=40°,则∠D的度数为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,边长为2的等边三角形ABC中,D点在边BC上运动(不与B、C重合),点E在边AB的延长线上,点F在边AC的延长线上,AD=DE=DF.
(1)若∠AED=30°,则∠ADB=_______°.
(2)求证:△BED≌△CDF
(3)点D在BC边上从B至C的运动过程中,△BED周长变化规律为( )
A.不变 B.一直变小 C.先变大后变小 D.先变小后变大

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(x-3)(x-2)-p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1、x2,且满足x12+x22=3 x1x2,求实数p的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com