Question

18．在平面直角坐标系中，直线y=x-3分别交x轴于B，交y轴于C，抛物线y=ax²-2ax+c经过点B、C两点，交x轴于另一点A
（1）求a、c的值；
（2）点P为直线BC下方抛物线上一点，PH⊥BC于H，PD∥y轴交BC于D，连接AD交y轴于E，连接BE，若BD=2DH，求BE的长；
（3）在（2）的条件下，连接BP，G为y轴正半轴上一点，BG绕点G逆时针旋转交抛物线第二象限上一点R，若$\frac{1}{2}$∠RGB=∠OBG+∠EBP，求点R的坐标．

Answer 1

分析 （1）首先求出B、C两点坐标，代入y=ax²-2ax+c中，解方程组即可．
（2）首先证明△DFB，△PDH都是等腰直角三角形，设DF=BF=a，则BD=$\sqrt{2}$a，DH=PH=$\frac{\sqrt{2}}{2}$a，PD=a，P（3-a，-2a），把P（3-a，-2a）代入y=x²-2x-3求得a=2或0（舍弃），推出P（1，-4），D（1，-2），OF=1，DF=2，由OE∥DF，得到$\frac{OE}{DF}$=$\frac{AO}{AF}$，求出OE，再利用勾股定理求出BE即可．
（3）如图2中，连接PB、RC、PC，作RH⊥y轴于H．只要证明△RHG≌△GOB，推出RH=OG，GH=OB=3，设OG=RH=m，则R（-m，3+m），把R（-m，3+m）代入y=x²-2x-3得3+m=m²+2m-3，解方程即可解决问题．

解答 解：（1）∵直线y=x-3分别交x轴于B，交y轴于C，
∴B（3，0），C（0，-3），
把B（3，0），C（0，-3）代入y=ax²-2ax+c得$\left\{\begin{array}{l}{c=-3}\\{9a-6a+c=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=1}\\{c=-3}\end{array}\right.$，
∴a=1，c=-3．

（2）如图1中，延长PD交x轴于F．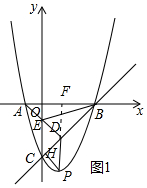

∵OC=OB=3，∠BOC=90°，
∴∠OCB=∠OBC=45°，
∵PH⊥BC，PF∥OC，
∴∠PDH=∠OCB=∠FDB=45°，
∴△DFB，△PDH都是等腰直角三角形，
设DF=BF=a，则BD=$\sqrt{2}$a，DH=PH=$\frac{\sqrt{2}}{2}$a，PD=a，
∴P（3-a，-2a），
把P（3-a，-2a）代入y=x²-2x-3得到，-2a=（3-a）²-2（3-a）-3，整理得a²-2a=0，解得a=2或0（舍弃），
∴P（1，-4），D（1，-2），
∴OF=1，DF=2，
∵OE∥DF，
∴$\frac{OE}{DF}$=$\frac{AO}{AF}$，
∴$\frac{OE}{2}$=$\frac{1}{2}$，
∴EO=1，
在Rt△OBE中，BE=$\sqrt{O{E}^{2}+O{B}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$．

（3）如图2中，连接PB、RC、PC，作RH⊥y轴于H．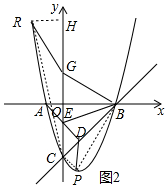

∵OE=1，OB=3，PC=$\sqrt{2}$，BC=3$\sqrt{2}$，
∴$\frac{OE}{OB}$=$\frac{PC}{BC}$=$\frac{1}{3}$，
∴$\frac{OE}{PC}$=$\frac{EB}{BC}$，∵∠BOE=∠PCB=90°，
∴△BOE∽△BCP，
∴∠OBE=∠CBP，
∴∠OBC=∠EBP=45°，
∵$\frac{1}{2}$∠RGB=∠OBG+∠EBP，又∵∠RGB=∠RGH+∠HGB=∠RGH+（∠GCB+∠GBC），
∴2∠OBG+2∠EBP=∠RGH+（∠GCB+∠GBC），
∴2∠OBG+90°=∠RGH+（45°+45°+∠OBG），
∴∠OBG=∠RGH，
∵RG=BG，∠RHG=∠GOB=90°，
∴△RHG≌△GOB，
∴RH=OG，GH=OB=3，设OG=RH=m，则R（-m，3+m），
把R（-m，3+m）代入y=x²-2x-3得3+m=m²+2m-3，解得m=2或-3（舍弃），
∴点R坐标为（-2，5）．

点评 本题考查二次函数综合题、等腰直角三角形的判定和性质、平行线的性质、相似三角形的判定和性质、全等三角形的判定和性质等知识，第三个问题的关键是，学会添加辅助线，构造全等三角形解决问题，学会利用参数构建方程，灵活运用待定系数法解决问题，属于中考压轴题．