

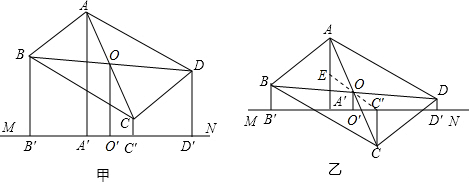
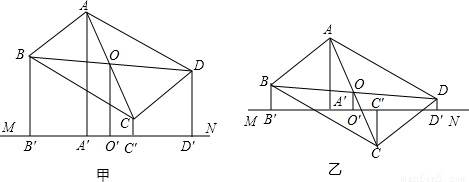
 (1)证明:∵O是BD中点,O'是B'D'的中点,
(1)证明:∵O是BD中点,O'是B'D'的中点, (BB′+DD′),OO′=
(BB′+DD′),OO′= (AA′+CC′),
(AA′+CC′), (BB′+DD′)=
(BB′+DD′)= (AA′+CC′),即AA'+CC'=BB'+DD';
(AA′+CC′),即AA'+CC'=BB'+DD'; A′E=
A′E= (AA′-CC′),
(AA′-CC′), (BB′+DD′),
(BB′+DD′), (BB′+DD′),OO′=
(BB′+DD′),OO′= (AA′+CC′)即可;
(AA′+CC′)即可; (AA′-CC′),OO′=
(AA′-CC′),OO′= (BB′+DD′),推出AA′-CC′=BB′+DD′即可.
(BB′+DD′),推出AA′-CC′=BB′+DD′即可.

 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2011-2012学年四川省内江市资中县陈家中心校九年级(上)期中数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2012年广东省惠州市中考数学模拟试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com