
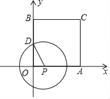
【题目】如图,正方形AOBC的顶点O在原点,边AO,BO分别在x轴和y轴上,点C坐标为(4,4),点D是BO的中点,点P是边OA上的一个动点,连接PD,以P为圆心,PD为半径作圆,设点P横坐标为t,当⊙P与正方形AOBC的边相切时,t的值为_____.
【答案】![]() 或2
或2![]()
【解析】
由点C的坐标可得OA、OB的长,根据点D是OB的中点可得OD的长,分⊙P与AC相切和⊙P与BC相切两种情况分别进行讨论即可求得答案.
∵点C坐标为(4,4),点D是BO的中点,
∴OA=OB=4,OD=![]() OB=2,
OB=2,
分⊙P与AC相切和⊙P与BC相切两种情况考虑:
①当⊙P与AC相切时,如图1所示.
∵点P横坐标为t,
∴PA=4﹣t.
在Rt△DOP中,OD=2,OP=t,PD=PA=4﹣t,
∴PD2=OD2+OP2,即(4﹣t)2=22+t2,
解得:t=![]() ;
;
②当⊙P与BC相切时,设切点为E,连接PE,如图2所示.
∵PE⊥BC,AC⊥BC,
∴PE∥AC.
∵PA∥EC,
∴四边形ACEP为矩形,
∴PE=AC=4,
∴PD=PE=4.
在Rt△POD中,OP=t,OD=2,PD=4,
∴PD2=OD2+OP2,即42=22+t2,
解得:t1=2![]() ,t2=﹣2
,t2=﹣2![]() (不合题意,舍去),
(不合题意,舍去),
综上所述:t的值为![]() 或2
或2![]() ,
,
故答案为:![]() 或2
或2![]() .
.


科目:初中数学 来源: 题型:
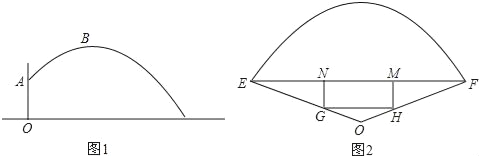
【题目】某公园在一个扇形OEF草坪上的圆心O处垂直于草坪的地上竖一根柱子OA,在A处安装一个自动喷水装置.喷头向外喷水.连喷头在内,柱高![]() m,水流在各个方向上沿形状相同的抛物线路径落下,喷出的水流在与D点的水平距离4米处达到最高点B,点B距离地面2米.当喷头A旋转120°时,这个草坪可以全被水覆盖.如图1所示.
m,水流在各个方向上沿形状相同的抛物线路径落下,喷出的水流在与D点的水平距离4米处达到最高点B,点B距离地面2米.当喷头A旋转120°时,这个草坪可以全被水覆盖.如图1所示.
(1)建立适当的坐标系,使A点的坐标为(O,![]() ),水流的最高点B的坐标为(4,2),求出此坐标系中抛物线水流对应的函数关系式;
),水流的最高点B的坐标为(4,2),求出此坐标系中抛物线水流对应的函数关系式;
(2)求喷水装置能喷灌的草坪的面积(结果用π表示);
(3)在扇形OEF的一块三角形区域地块△OEF中,现要建造一个矩形GHMN花坛,如图2的设计方案是使H、G分别在OF、OE上,MN在EF上.设MN=2x,当x取何值时,矩形GHMN花坛的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3个完全相同的小球,把它们分别标号为1,2,3,放在一个口袋中,随机地摸出一个小球不放回,再随机地摸出一个小球.
(1) 采用树形图法(或列表法)列出两次摸球出现的所有可能结果;
(2) 求摸出的两个球号码之和等于5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
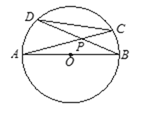
【题目】如图,⊙O的直径AB=10,CD是⊙O的弦,AC与BD相交于点P.
(1)设∠BPC=α,如果sinα是方程5x2-13x+6=0的根,求cosα的值;
(2)在(1)的条件下,求弦CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a=2 002x+2 003,b=2 002x+2 004,c=2 002x+2 005,则多项式a2+b2+c2-ab-bc-ca的值为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
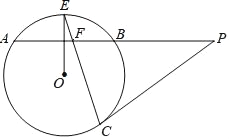
【题目】如图,AB是⊙O的弦,半径OE⊥AB,P为AB的延长线上一点,PC与⊙O相切于点C,CE与AB交于点F.
(1)求证:PC=PF;
(2)连接OB,BC,若OB∥PC,BC=3![]() ,tanP=
,tanP=![]() ,求FB的长.
,求FB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某汽车在路面上朝正东方向匀速行驶,在A处观测到楼H在北偏东60°方向上,行驶1小时后到达B处,此时观测到楼H在北偏东30°方向上,那么该车继续行驶( )分钟可使汽车到达离楼H距离最近的位置.
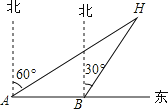
A.60 B.30 C.15 D.45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作出反比例函数y=-![]() 的图象,并结合图象回答:(1)当x=2时,y的值;(2)当1<x≤4时,y的取值范围;(3)当1≤y<4时,x的取值范围.
的图象,并结合图象回答:(1)当x=2时,y的值;(2)当1<x≤4时,y的取值范围;(3)当1≤y<4时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
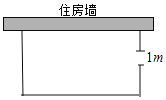
【题目】如图,一农户要建一个矩形鸭舍,鸭舍的一边利用长为13m的住房墙,另外三边用27m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门![]() 所围矩形鸭舍的长、宽分别为多少时,鸭舍面积为
所围矩形鸭舍的长、宽分别为多少时,鸭舍面积为![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com