
【题目】已知:如图,⊙A与y轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为![]() ,过点C作⊙A的切线交x轴于点B(-4,0).
,过点C作⊙A的切线交x轴于点B(-4,0).
(1)求切线BC的解析式;
(2)若点P是第一象限内⊙A上的一点,过点P作⊙A的切线与直线BC相交于点G,且∠CGP=120°,求点G的坐标.

【答案】(1)![]() ;(2)G(
;(2)G(![]() ,
,![]() +2 ).
+2 ).
【解析】
(1)连接AC,由于BC与⊙A相切,则AC⊥BC,在Rt△ABC中,OC⊥AB,根据射影定理即可求得OC的长,从而得到C点的坐标,进而用待定系数法求出直线BC的解析式.
(2)可设出G点的坐标(设横坐标,利用直线BC的解析式表示纵坐标),连接AP、AG;由于GC、GP都是⊙A的切线,那么∠AGC=∠ABP=60°,在Rt△AGC中,AC的长易求得,根据∠AGC的度数,即可求得AG的长;过G作GH⊥x轴于H,在Rt△GAH中,可根据G点的坐标表示出AH、GH的长,进而由勾股定理求得G点的坐标.
解:(1)如图1所示,连接AC,则AC=![]() .
.
在Rt△AOC中,AC=![]() ,OA=1,则OC=2,
,OA=1,则OC=2,
∴点C的坐标为(0,2).
设切线BC的解析式为y=kx+b,
它过点C(0,2),B(﹣4,0),
则有![]() ,
,
解之得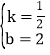 ,
,
∴![]() ;
;
(2)如图1所示,设点G的坐标为(a,c),
∵点G在直线y=![]() x+2上,
x+2上,
∴c=![]() a+2,
a+2,
过点G作GH⊥x轴,垂足为H点,则OH=a,GH=c=![]() a+2,连接AP,AG.
a+2,连接AP,AG.
∵AC=AP,AG=AG,所以Rt△ACG≌Rt△APG (HL),
∴∠AGC=![]() ×120°=60°.
×120°=60°.
在Rt△ACG中,
∵∠AGC=60°,AC=![]() ,
,
∴sin60°=![]() ,
,
∴AG=![]() .
.
在Rt△AGH中,AH=OH﹣OA=a﹣1,GH=![]() a+2,
a+2,
∵AH2+GH2=AG2,
∴(a﹣1)2+![]() =
=![]() ,
,
解之得:a1=![]() ,a2=﹣
,a2=﹣![]() (舍去),
(舍去),
点G的坐标为(![]() ,
,![]() +2 ).
+2 ).


科目:初中数学 来源: 题型:
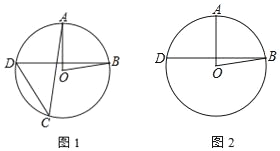
【题目】如图,在⊙O中,半径OA与弦BD垂直,点C在⊙O上,∠AOB=80°
(1)若点C在优弧BD上,求∠ACD的大小;
(2)若点C在劣弧BD上,直接写出∠ACD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
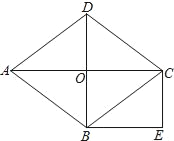
【题目】如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长;
(2)求四边形OBEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)若BC=4,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
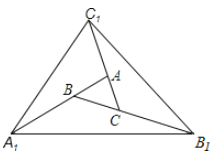
【题目】如图,对面积为S的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2、B2、C2,得到△A2B2C2,记其面积为S2;··· ;则![]() ______. 按此规律继续下去,可得到
______. 按此规律继续下去,可得到![]() ,则其面积
,则其面积![]() _______.
_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
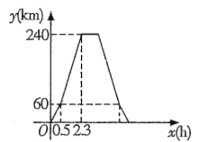
【题目】一辆快递车从长春出发,走高速公路,途经伊通,前往靖宇镇送快递,到达后卸货和休息共用![]() ,然后开车按原速原路返回长春.这辆快递车在长春到伊通、伊通到靖宇的路段上分别以不同的速度保持匀速前进,返回时也分别按原速返回.这辆快递车距离长春的路程
,然后开车按原速原路返回长春.这辆快递车在长春到伊通、伊通到靖宇的路段上分别以不同的速度保持匀速前进,返回时也分别按原速返回.这辆快递车距离长春的路程![]() 与它行驶的时间
与它行驶的时间![]() 之间的函数图象如图所示.
之间的函数图象如图所示.
(1)快递车从伊通到长春的速度是__________![]() ,快递车从长春到靖宇镇往返一共用了__________
,快递车从长春到靖宇镇往返一共用了__________![]() ;
;
(2)当这辆快递车在靖宇到伊通的路段上行驶时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)如果这辆快递车两次经过同一个服务区的时间间隔为![]() ,直接写出这个服务区距离伊通的路程.
,直接写出这个服务区距离伊通的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
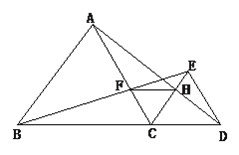
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD;
②求证:CF=CH;
③判断△CFH的形状并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=CB,O是AB的中点,CA与⊙O相切于点E,CO交⊙O于点D
(1)求证:CB是⊙O的切线;
(2)若∠ACB=80°,点P是⊙O上一个动点(不与D,E两点重合),求∠DPE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com