
 如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.| α | sinα | cosα | tanα |
| 25° | 0.42 | 0.91 | 0.47 |
| 37° | 0.60 | 0.80 | 0.75 |
分析 作CH⊥AB,求得CH=AC•sin∠CAB≈4.20千米、AH=AC•cos∠CAB≈9.10千米,继而求得BH=CH÷tan∠CBA≈5.60千米,根据AB=AH+BH可得答案.
解答 解:作CH⊥AB于点H.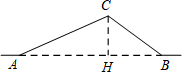
在Rt△ACH中,CH=AC•sin∠CAB=AC•sin25°≈10×0.42=4.20千米,
AH=AC•cos∠CAB=AC•cos25°≈10×0.91=9.10千米,
在Rt△BCH中,BH=CH÷tan∠CBA=4.2÷tan37°≈4.2÷0.75=5.60千米,
∴AB=AH+BH=9.10+5.60=14.70≈14.7千米.
故改直的公路AB的长约为14.7千米.
点评 本题主要考查解直角三角形的应用,熟练掌握三角函数的定义是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
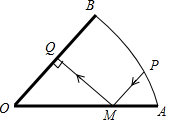 两面镜OA、OB如图放置,OA=OB=10cm,点P是$\widehat{AB}$上,PM为入射光线,且PM∥OB.
两面镜OA、OB如图放置,OA=OB=10cm,点P是$\widehat{AB}$上,PM为入射光线,且PM∥OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由a>b,且c≠0,得ac<bc | B. | 若x>y,且m≠0,则-$\frac{x}{m}<-\frac{y}{m}$ | ||
| C. | 若x>y,则xz2>yz2 | D. | 若an2>bn2,则a>b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com