
分析 (1)一元二次方程的二次项的系数不等于0,故a=0时,不是一元二次方程;
(2)根据一元二次方程的定义可得3x2+2mx=6是一元二次方程,再根据一般式ax2+bx+c=0,其中ax2叫做二次项,a叫做二次项系数;bx叫做一次项;c叫做常数项.一次项系数b和常数项c可取任意实数可得答案;
(3)根据一元二次方程的定义可得(b2+1)x2-bx+b=2是一元二次方程,再根据一般式ax2+bx+c=0,其中ax2叫做二次项,a叫做二次项系数;bx叫做一次项;c叫做常数项.一次项系数b和常数项c可取任意实数可得答案;
(4)一元二次方程的二次项的系数不等于0,故m=1时,不是一元二次方程.
解答 解:(1)ax2+2bx=$\sqrt{3}$,当a=0时,不是一元二次方程,当a≠0时是一元二次方程;
(2)3x2+2mx=6是一元二次方程,
一般形式:3x2+2mx-6=0,
二次项系数3,一次项系数2m,常数项-6;
(3)(b2+1)x2-bx+b=2是一元二次方程,
一般式:(b2+1)x2-bx+b-2=0,
二次项系数b2+1,一次项系数-b,常数项b-2;
(4)mx2+2mx=x2+m-1,当m=1时,不是一元二次方程,当m≠1时是一元二次方程.
点评 本题利用了一元二次方程的概念.只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程,一般形式是ax2+bx+c=0(且a≠0).特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
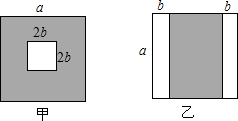 如图,有甲、乙两种边长为a的正方形印花砖,阴影部分代表印花区域,空白部分代表留白区域,甲的留白区域是正方形,乙的留白区域是两个长方形.
如图,有甲、乙两种边长为a的正方形印花砖,阴影部分代表印花区域,空白部分代表留白区域,甲的留白区域是正方形,乙的留白区域是两个长方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com