
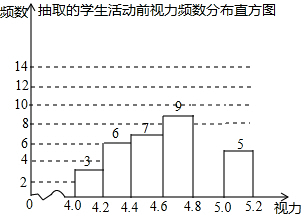
 为了保护视力,学校计划开展“爱眼护眼”视力保健活动,为使活动更具有实效性,先对学生视力情况进行调查,随机抽取40名学生,检查他们的视力,并绘制不完整的直方图(数据包括左端点不包括右端点,精确到0.1),请结合直方图的信息解答下列问题:
为了保护视力,学校计划开展“爱眼护眼”视力保健活动,为使活动更具有实效性,先对学生视力情况进行调查,随机抽取40名学生,检查他们的视力,并绘制不完整的直方图(数据包括左端点不包括右端点,精确到0.1),请结合直方图的信息解答下列问题:分析 (1)根据各组频数之和等于总数可得答案;
(2)由(1)中所求结果即可补全;
(3)用360°乘以视力达到4.8及以上得人数所占比例;
(4)用800乘以视力达到4.8及以上得人数所占比例.
解答 解:(1)4.8≤x<5.0的学生数是40-(3+6+7+9+5)=10(人),
故答案为:10;
(2)补全频数分布直方图如下: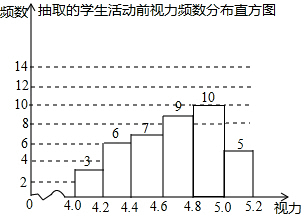
(3)视力达标学生所对应扇形的圆心角度数为360°×$\frac{10+5}{40}$=135°,
故答案为:135;
(4)若全校共有800名学生,则视力达标的学生估计有800×$\frac{10+5}{40}$=300,
故答案为:300.
点评 本题考查频数直方图、用样本估计总体的思想、统计量的选择等知识,解题的关键是搞清楚频数、达标等概念.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
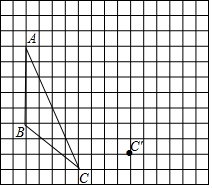 画图并填空,如图:方格纸中每个小正方形的边长都为1,△ABC的顶点都在方格纸的格点上,将△ABC经过一次平移后得到△A'B'C'.图中标出了点C的对应点C'.
画图并填空,如图:方格纸中每个小正方形的边长都为1,△ABC的顶点都在方格纸的格点上,将△ABC经过一次平移后得到△A'B'C'.图中标出了点C的对应点C'.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4<m<5 | B. | 4≤m<5 | C. | 4<m≤5 | D. | 4≤m≤5 |
查看答案和解析>>
科目:初中数学 来源:2017届广东省梅州市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
某校学生会就全校1000名同学周末期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成条形统计图.
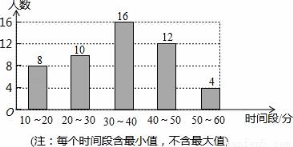
(1)求样本容量,并估计全校同学在周末期间平均每夭做家务活的时间在40分钟以上(含40分钟)的人数;
(2)校学生会拟在表现突出的A、B、C、D四名同学中,随机抽取两名同学向全校汇报.请用树状图或列表法表示出所有可能的结果,并求恰好抽到A、B两名同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com