
科目:初中数学 来源: 题型:解答题
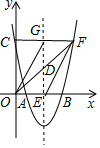 如图,过点F(6,5)的抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C.且B(5,0)
如图,过点F(6,5)的抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C.且B(5,0)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小梅家的阳台上放置了一个晒衣架,如图1和如图2是晒衣架的侧面示意图,A、B两点立于地面,将晒衣架稳固张开,测得张角∠AOB=62°,立杆OA=OB=135cm,小梅的连衣裙穿在衣架后的总长度为115cm,问将这件连衣裙垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)
小梅家的阳台上放置了一个晒衣架,如图1和如图2是晒衣架的侧面示意图,A、B两点立于地面,将晒衣架稳固张开,测得张角∠AOB=62°,立杆OA=OB=135cm,小梅的连衣裙穿在衣架后的总长度为115cm,问将这件连衣裙垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=$\frac{1}{2}$x+2与x轴和y轴分别相交于A、B两点,把△AOB绕原点顺时针旋转90°得到△COD,且抛物线y=ax2b+x+c过A、C、D三点.
如图,直线y=$\frac{1}{2}$x+2与x轴和y轴分别相交于A、B两点,把△AOB绕原点顺时针旋转90°得到△COD,且抛物线y=ax2b+x+c过A、C、D三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com