
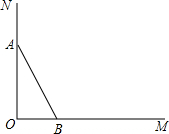
 如图,一根木棒(AB)长2a,斜靠在与地面(OM)垂直的墙壁(ON)上,与地面的倾斜角(∠ABO)为60°.若木棒A端沿直线ON下滑,且B端沿直线OM向右滑行(NO⊥OM),于是木棒的中点P也随之运动,已知A端下滑到A′时,AA′=(
如图,一根木棒(AB)长2a,斜靠在与地面(OM)垂直的墙壁(ON)上,与地面的倾斜角(∠ABO)为60°.若木棒A端沿直线ON下滑,且B端沿直线OM向右滑行(NO⊥OM),于是木棒的中点P也随之运动,已知A端下滑到A′时,AA′=(| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| OA′ |
| A′B′ |
| ||
| 2 |
| 15•π•a |
| 180 |
| 1 |
| 12 |
| 1 |
| 12 |
| nπR |
| 180 |


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
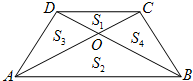 某生活小区临街的一面有块如图所示的梯形空地,物业部门打算把这块空地美化一下,以供观赏.初步打算沿对角线AC,BD修两条小路,把梯形ABCD分成四块,种上相同种类的花.四块地的面积分别为S1,S2,S3,S4,一位物业工人很快看出S3,S4两种需要花的棵数大致相等.
某生活小区临街的一面有块如图所示的梯形空地,物业部门打算把这块空地美化一下,以供观赏.初步打算沿对角线AC,BD修两条小路,把梯形ABCD分成四块,种上相同种类的花.四块地的面积分别为S1,S2,S3,S4,一位物业工人很快看出S3,S4两种需要花的棵数大致相等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com