
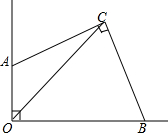
 如图,若∠AOB=∠ACB=90°,OC平分∠AOB.
如图,若∠AOB=∠ACB=90°,OC平分∠AOB.分析 ①作CN⊥OA,CM⊥OB,证得△CAN≌△CMB,即可得出结论;
②利用勾股定理求得正方形CNOM的边长,即可求得面积.
解答 解:①如图,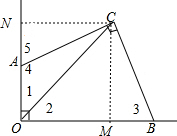
作CN⊥OA,CM⊥OB,
∵∠AOB=∠ACB=90°,
∴∠3+∠4=180°
∵∠5+∠4=180°
∴∠3=∠5
∵OC平分∠AOB
∴CM=CN
在△CAN和△CMB中,
$\left\{\begin{array}{l}{∠3=∠5}\\{∠ANC=∠CMB=90°}\\{CM=CN}\end{array}\right.$,
∴△CAN≌△CMB,
∴四边形CNOM就是拼成的正方形,
∴四边形AOBC的面积等于正方形CNOM.
②设正方形CNOM的边长为x,OC=2,由勾股定理可知:
x2+x2=4,
x2=2
∴四边形AOBC的面积等于2.
点评 此题考查图形的剪拼,全等三角形的判定与性质,勾股定理的运用,正确作出辅助线,证得三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 如图,蚂蚁在距巢穴2米远找到一只苍蝇,决定将其搬回家,可蚂蚁每一分钟内前进1米,却被风刮退2米,请问这只蚂蚁能否回到巢穴?如不能,请说明理由;如能,算一算何时能回巢穴.
如图,蚂蚁在距巢穴2米远找到一只苍蝇,决定将其搬回家,可蚂蚁每一分钟内前进1米,却被风刮退2米,请问这只蚂蚁能否回到巢穴?如不能,请说明理由;如能,算一算何时能回巢穴.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图为一个正方体的展开图,图中已标出三个面在正方体中的位置f表示前面,r表示右面,d表示下面.试判定另外三个面a、b、c在正方体中的位置.
如图为一个正方体的展开图,图中已标出三个面在正方体中的位置f表示前面,r表示右面,d表示下面.试判定另外三个面a、b、c在正方体中的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在矩形ABCD中,AB=2,BC=1,P为矩形ABCD的边上的一个动点,它从点A出发,沿A→B→C运动.设点P经过的路程为x,三角形APC的面积为S.当x等于多少时,三角形APC的面积S等于$\frac{1}{2}$?
已知:如图,在矩形ABCD中,AB=2,BC=1,P为矩形ABCD的边上的一个动点,它从点A出发,沿A→B→C运动.设点P经过的路程为x,三角形APC的面积为S.当x等于多少时,三角形APC的面积S等于$\frac{1}{2}$?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,DA、CB是⊙O的切线,CD切⊙O于E.
如图,AB是⊙O的直径,DA、CB是⊙O的切线,CD切⊙O于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
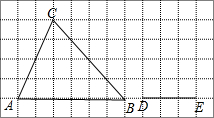 如图,在12×6的正方形网格中,点A,B,C,D,E均在格点上,以DE为一边画格点△DEF,使得△DEF∽△ABC.其中AB=6,AC=2$\sqrt{5}$,BC=4$\sqrt{2}$,DE=3.
如图,在12×6的正方形网格中,点A,B,C,D,E均在格点上,以DE为一边画格点△DEF,使得△DEF∽△ABC.其中AB=6,AC=2$\sqrt{5}$,BC=4$\sqrt{2}$,DE=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com