
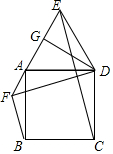
 如图,正方形ABCD,过A作直线AE,过D作DG⊥AE,AG=GE,连DE.
如图,正方形ABCD,过A作直线AE,过D作DG⊥AE,AG=GE,连DE.分析 (1)根据线段垂直平分线的性质得:DE=AD,由正方形的边长相等得:AD=CD,则DE=DC;
(2)作辅助线,构建全等三角形,先证明∠GDF=∠ADB=45°,得△FDG是等腰直角三角形,则FD=$\sqrt{2}$FA+$\sqrt{2}$AG,再证明△ABH≌△DAG,得AG=BH,DG=AH,所以△BHF是等腰直角三角形,则FB=$\sqrt{2}$BH=$\sqrt{2}$AG,可得结论;
解答 证明:(1)∵DG⊥AE,AG=EG,
∴DG是AE的垂直平分线,
∴DE=AD,
∵四边形ABCD是正方形,
∴AD=DC,
∴DE=DC;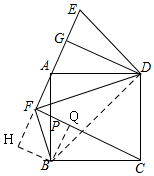
(2)解:过B作BH⊥EF,交EF延长线于H,连接BD,
∵四边形ABCD是正方形,
∴BD平分∠ADC,
∴∠ADB=∠CDB=45°,
∵AD=DE,DG⊥AE,
∴∠ADG=∠EDG,
∴∠ADG+∠ADB=∠EDG+∠BDC=$\frac{1}{2}$∠EDC,
∵DF平分∠EDC,
∴∠FDC=∠EDF=$\frac{1}{2}$∠EDC,
∴∠FDC=∠ADG+∠ADB=∠BDF+∠BDC,
∴∠ADG=∠BDF,
∴∠GDF=∠ADB=45°,
∵DG⊥EF,
∴△FDG是等腰直角三角形,
∴FD=$\sqrt{2}$FG=$\sqrt{2}$(FA+AG)=$\sqrt{2}$FA+$\sqrt{2}$AG,
∵∠BAD=90°,
∴∠HAB+∠DAG=90°,
∵∠AGD=90°,
∴∠DAG+∠ADG=90°,
∴∠HAB=∠ADG,
∵AB=AD,∠AHB=∠AGD=90°,
∴△ABH≌△DAG,
∴AG=BH,DG=AH,
∵△FDG是等腰直角三角形,
∴GD=FG,
∴FG=AH,
∴FA+AG=FA+FH,
∴AG=FH,
∵AG=BH,
∴FH=BH,
∴△BHF是等腰直角三角形,
∴FB=$\sqrt{2}$BH=$\sqrt{2}$AG,
∴FD-$\sqrt{2}$AG=$\sqrt{2}$FA,
∴FD-FB=$\sqrt{2}$FA;
点评 本题是四边形的综合题,考查了正方形的性质、矩形的性质和判定、三角形全等的性质和判定、勾股定理、等腰直角三角形的性质和判定,熟练掌握等腰直角三角形斜边是一直角边的 $\sqrt{2}$倍是关键,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| 队员1 | 队员2 | 队员3 | 队员4 | 队员5 | 队员6 | |
| 甲组 | 176 | 177 | 175 | 176 | 177 | 175 |
| 乙组 | 178 | 175 | 170 | 174 | 183 | 176 |
| A. | $\overline{x}$甲=$\overline{x}$乙,S甲2<S乙2 | B. | $\overline{x}$甲=$\overline{x}$乙,S甲2>S乙2 | ||
| C. | $\overline{x}$甲<$\overline{x}$乙,S甲2<S乙2 | D. | $\overline{x}$甲>$\overline{x}$乙,S甲2>S乙2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
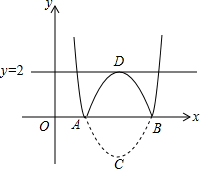 抛物线y=x2+bx+c与x轴交于点A、B,顶点为C,若将此抛物线沿x轴向上翻折,使点C落在点D处,得到如图所示图形记作图形F.
抛物线y=x2+bx+c与x轴交于点A、B,顶点为C,若将此抛物线沿x轴向上翻折,使点C落在点D处,得到如图所示图形记作图形F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{m=4}\\{n=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{m=2}\\{n=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{m=-2}\\{n=-4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{m=-4}\\{n=-2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3xy2)3=9x3y6 | B. | B、(x+y)2=x2+y2 | ||
| C. | x6÷x2=x3 | D. | 2x2y-$\frac{1}{2}$yx2=$\frac{3}{2}$x2y |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ±1 | B. | 1 | C. | 4-3$\sqrt{3}$ | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 班级 | 九年一班 | 九年二班 | 九年三班 | 九年四班 |
| 人数 | 36 | 36 | 42 | 46 |
| A. | 40、39 | B. | 36、40 | C. | 39、39 | D. | 39、40 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com